UStepper Robot Arm 4: 5 kroků

2024 Autor: John Day | [email protected]. Naposledy změněno: 2024-01-30 08:21

Toto je čtvrtá iterace mé robotické paže, kterou jsem vyvinul jako aplikaci pro naši řídicí desku krokového ovladače uStepper. Protože robot má 3 krokové motory a servo pro ovládání (v základní konfiguraci), není omezen na uStepper, ale může být použit s jakoukoli deskou krokového ovladače.

Konstrukce vychází z průmyslového paletizačního robota - a je relativně jednoduchá. S tím bylo řečeno, strávil jsem nespočet hodin vymýšlením designu a optimalizací jak pro snadnou montáž, tak také pro snadný tisk dílů.

Design jsem udělal s ohledem na snadný tisk a jednoduchost montáže. Ne, že by nebylo možné tyto dva parametry zlepšit, ale myslím, že jsem ušel dlouhou cestu. Kromě toho bych chtěl stáhnout průmyslovou robotiku na úroveň, kde ji mohou fanoušci sledovat, a ukázat, že to lze udělat poměrně jednoduše - a také matematiku k ovládání!

Neváhejte zanechat komentář s konstruktivní zpětnou vazbou na design, ale především na to, jak to dělám, aby byl přístupný všem (zejména matematice).

Krok 1: Požadované součásti, 3D tisk a montáž

V zásadě vše, co potřebujete vědět, je v montážním manuálu. K dispozici je podrobný kusovník se zakoupenými i vytištěnými díly a podrobný montážní návod.

3D tisk se provádí na přiměřené kvalitě 3D tiskárny (FDM) s výškou vrstvy 0,2 mm a 30 % výplní. Nejnovější iteraci dílů a pokyny najdete zde:

Krok 2: Kinematika

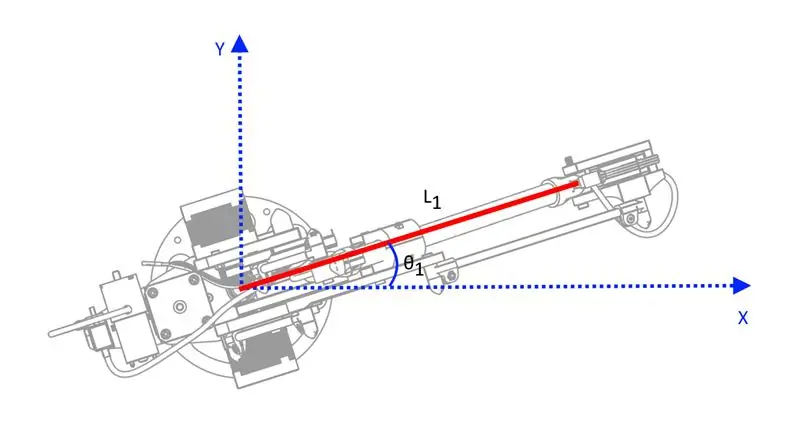
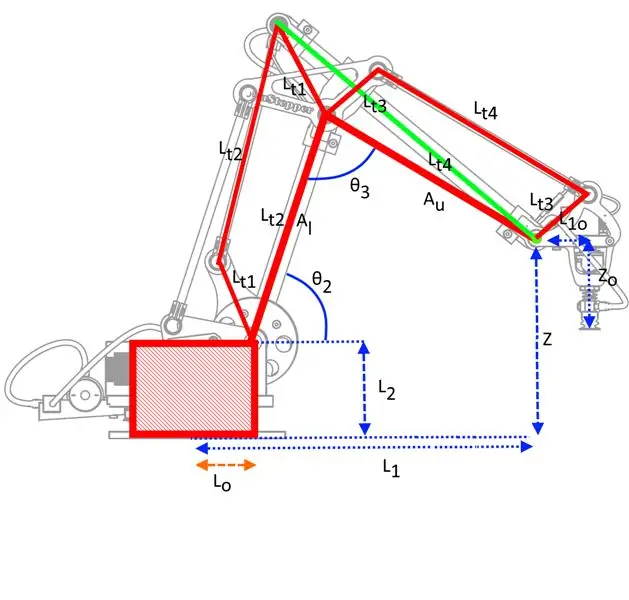
Chcete -li, aby se paže pohybovala předvídatelným způsobem, musíte udělat matematiku: OI jsem hledal na mnoha místech relativně jednoduchý popis kinematiky související s tímto typem robota, ale nenašel jsem žádný, o kterém se domnívám, že byl na úroveň, které většina lidí rozuměla. Udělal jsem svou vlastní verzi kinematiky založenou výhradně na trigonometrii a ne na maticových transformacích, které se mohou zdát docela děsivé, pokud jste na tom nikdy předtím nepracovali - jsou však pro tohoto konkrétního robota docela jednoduché, protože jsou to jen 3 DOF.

Přesto si myslím, že můj přístup v přiloženém dokumentu je napsán poměrně snadno srozumitelným způsobem. Ale podívejte se, jestli vám to dává smysl!

Krok 3: Kódování kinematiky

Kinematiku lze těžko pochopit i při výpočtech, které jsem poskytl v prvním. Zde je tedy především implementace Octave - Octave je bezplatný nástroj s mnoha stejnými funkcemi, jaké najdete v Matlabu.

L1o = 40; Zo = -70; L_2 = 73,0; Au = 188,0; Al = 182,0; Lo = 47,0; UPPERARMLEN = Au; LOWERARMLEN = Al; XOFFSET = Lo; ZOFFSET = L_2; AZOFFSET = Zo; AXOFFSET = L1o; disp ('Implementace kódu') disp ('Vstupní úhly:') rot = deg2rad (30); vpravo = deg2rad (142,5); vlevo = deg2rad (50); rad2deg (rot) rad2deg (vpravo) rad2deg (vlevo) T1 = rot; #base T2 = vpravo; #shoulder T3 = vlevo; #elbow #FW kinematika pro získání XYZ z úhlů: disp ('Vypočítané X, Y, Z:') z = ZOFFSET + sin (vpravo)*LOWERARMLEN - cos (vlevo - (pi/2 - vpravo))*UPPERARMLEN + AZOFFSET k1 = sin (vlevo - (pi/2 - vpravo))*UPPERARMLEN + cos (vpravo)* LOWERARMLEN + XOFFSET + AXOFFSET; x = cos (rot)*k1 y = sin (rot)*k1 ## inverzní kinematika pro získání úhlů z XYZ: rot = atan2 (y, x); x = x - cos (rot)*AXOFFSET; y = y - sin (rot)*AXOFFSET; z = z - AZOFFSET -ZOFFSET; L1 = sqrt (x*x + y*y) - XOFFSET; L2 = sqrt ((L1)*(L1) + (z)*(z)); a = (z)/L2; b = (L2*L2 + LOWERARMLEN*LOWERARMLEN - UPPERARMLEN*UPPERARMLEN)/(2*L2*LOWERARMLEN); c = (LOWERARMLEN*LOWERARMLEN + UPPERARMLEN*UPPERARMLEN - L2*L2)/(2*LOWERARMLEN*UPPERARMLEN); vpravo = (atan2 (a, sqrt (1-a*a)) + atan2 (sqrt (1-b*b), b)); vlevo = atan2 (sqrt (1-c*c), c); ## výstup vypočtené úhly disp ('výstupní úhly:') rot = rad2deg (rot) vpravo = rad2deg (vpravo) left = rad2deg (vlevo)

S výše uvedeným skriptem máte v podstatě připravený implementační kód pro dopřednou a zpětnou kinematiku.

Forward Kinematics, kterou používáte pro výpočet, kde skončíte s danou sadou úhlů motoru. Inverzní kinematika poté (provede inverzní) vypočítá, jaké úhly motoru potřebujete, abyste skončili v požadované poloze x, y, z. Poté je třeba vložit omezení pohybu motoru, jako např. rotační základna se může pohybovat pouze od 0 do 359 stupňů. Tímto způsobem zajistíte, že se nedostanete na pozice, které nejsou proveditelné.

Krok 4: Spuštění věci

Nejsme úplně tam s implementací kinematické knihovny, takže zatím nemohu poskytnout. Ale můžu vám ukázat video, jak to běží. Je to docela stabilní a plynulé díky použití ložisek a řemenového pohonu, kromě rozumné kvality pohonů, které jsou zde desky uStepper S.

Krok 5: Další koncové efektory

Navrhl jsem 3 další koncové efektory. Jeden je jednoduše horizontální chapadlo, druhý se hodí k běžnému evropskému plechovce od piva nebo sody a nakonec je zde vakuový systém chapadel, který vám umožní namontovat na vakuový pohár, pumpu a ventil.

Všechny budou nebo jsou k dispozici zde (soubory 3D STL a pokyny):