Jak vytvořit geodetický dóm ve stylu Temcor v aplikaci Autodesk Inventor: 8 kroků

2025 Autor: John Day | [email protected]. Naposledy změněno: 2025-01-13 06:57

Tento tutoriál vám ukáže, jak vytvořit kopuli ve stylu Temcor pomocí jen trochu matematiky.

Většina informací v tomto tutoriálu byla získána z TaffGochova reverzního inženýrství metody dělení staré stanice Amundsen-Scott South Pole Station, takže mu patří obrovské díky!

Hlavní výhodou kopulí Temcor je jejich nízký počet unikátních vzpěr - zvyšuje se aritmeticky s frekvencí, ne na rozdíl od pravidelné triakontaedrické geodetické mřížky Duncana Stuarta (metoda 3*), ale výsledek vypadá mnohem příjemněji.

Pro jednoduchost je frekvence kopule, kterou vytváříme, 14, takže akordové faktory lze porovnat s modelem TaffGoch's Temcor.

. Ipt aplikace Inventor 2016 je zahrnut na konci výukového programu.

*AKTUALIZACE*

Metodu 4 jsem popsal jako pravidelnou triakontaedrální geodetickou mřížku Duncana Stuarta, ale není. Metodu ve skutečnosti vynalezl Christopher Kitrick, který ve své práci z roku 1985 „Geodesic Domes“popsal její konstrukci. Kromě toho ve svém příspěvku z roku 1990 „Sjednocený přístup k geodetickým kopulím třídy I, II a III“nastiňuje dalších 8 metod, jednou z nich je metoda 3 Duncana Stuarta, druhou vlastní „metoda 4“a překvapivě dost, analogická metoda pro Temcor's, kterou nazývá „Metoda aa“(krok 7 ukazuje, jak Temcor upravil „Metodu aa“). V budoucnosti, které lze instruovat, popíši konstrukci metod popsaných ve druhém příspěvku.

Krok 1: Uživatelské parametry

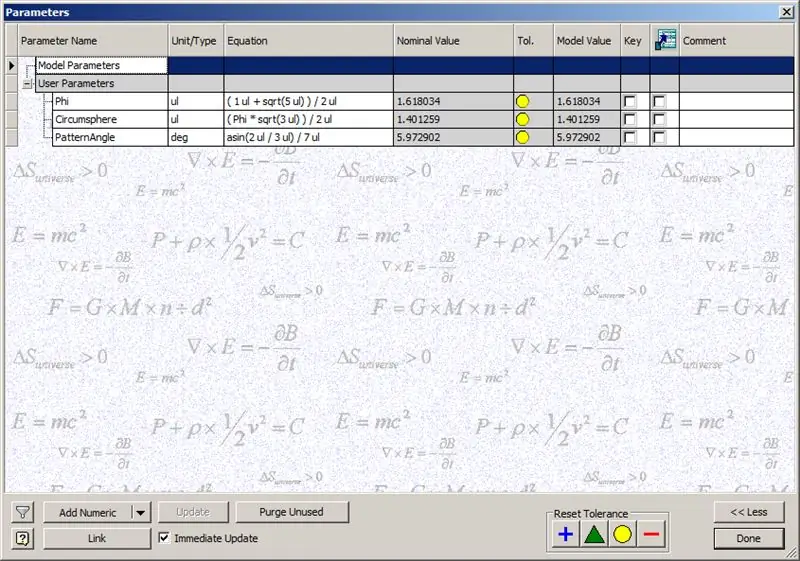
Než se pustíme do stavby kopule, zadejte zobrazené parametry:

Phi - Zlatý poměr. Definováno jako ((1+√5/) 2

Circumsphere - toto je cirkule sféry dvanáctistěnu, definovaného jako ((Phi*√3)/2)

PatternAngle - Toto je centrální úhel dvanáctistěnu. Protože frekvence naší kopule je 14, dělíme tento středový úhel polovinou frekvence, v tomto případě 7.

Krok 2: Načrtnutí zlatého obdélníku

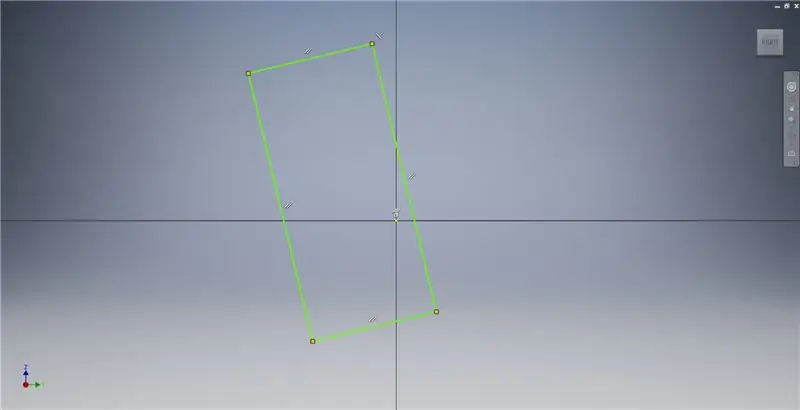
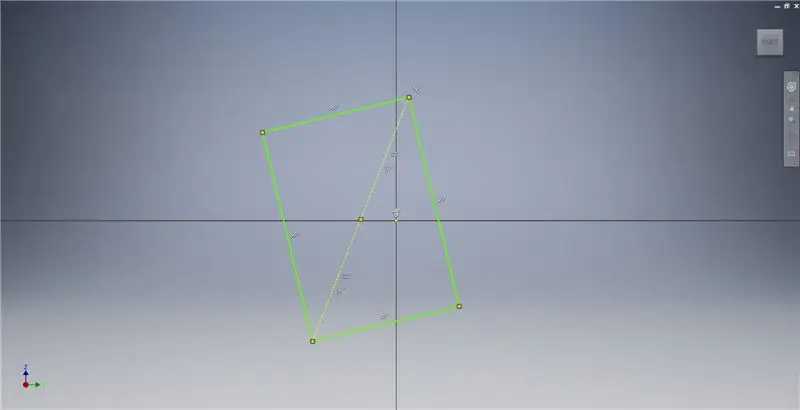
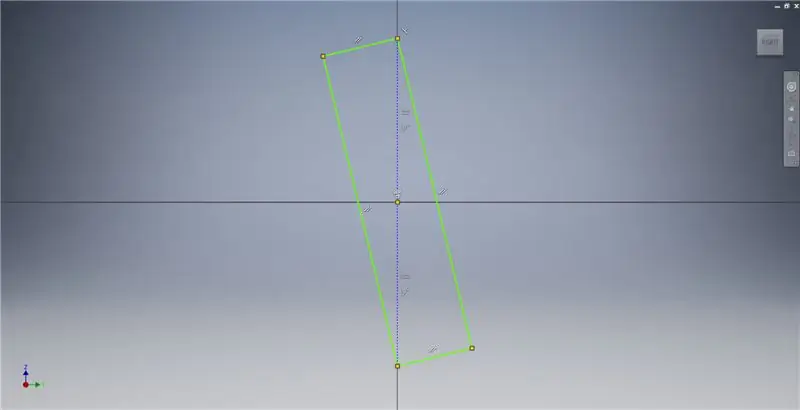
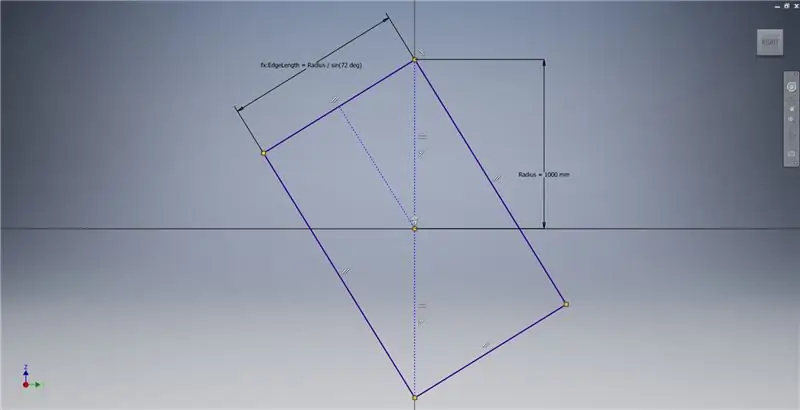
Začněte náčrtem v rovině YZ a poté vytvořte tříbodový obdélník, jak je znázorněno na obrázku, v poznámkách k obrázku najdete další informace popisující vytvoření zlatého obdélníku.

Krok 3: Vytvoření obdélníku Golden²

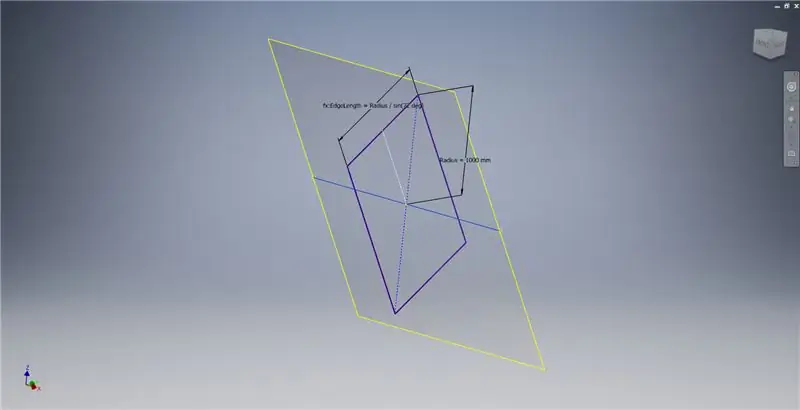
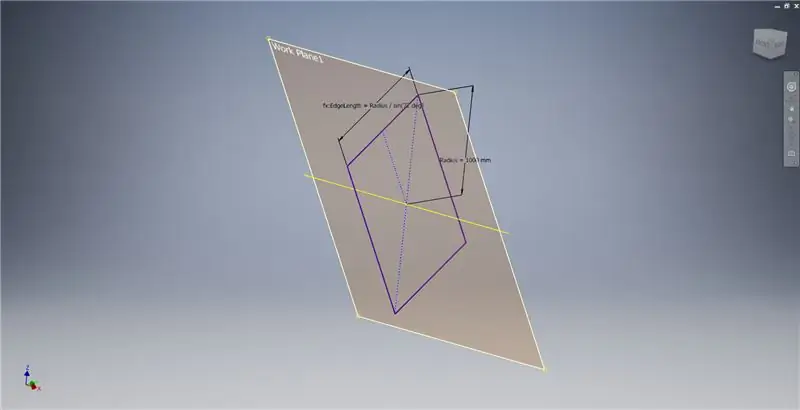
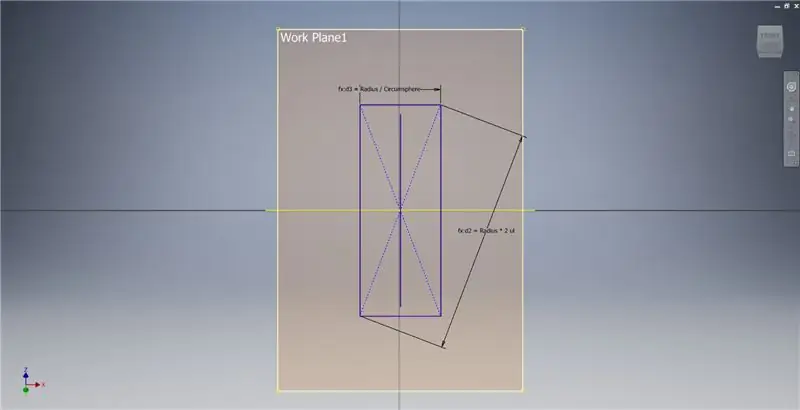
Vytvořte pracovní rovinu pomocí osy X a čáry zvýrazněné na prvním obrázku, poté spusťte další skicu v této pracovní rovině. Vytvořte obdélník se středovým bodem počínaje od počátku a poté obdélník okótujte podle obrázku na třetím obrázku.

Krok 4: Vytvoření 2v Triacon Triangle

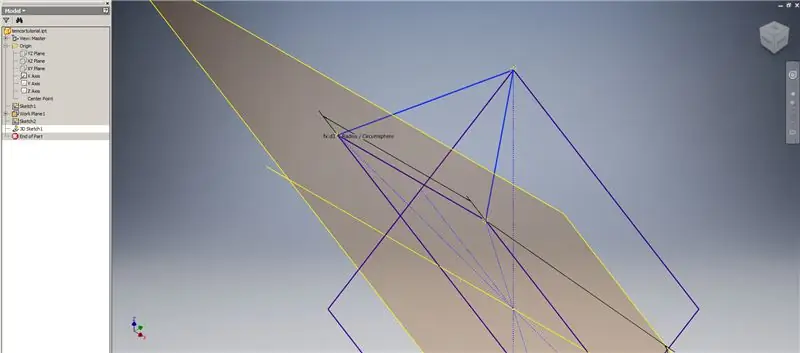
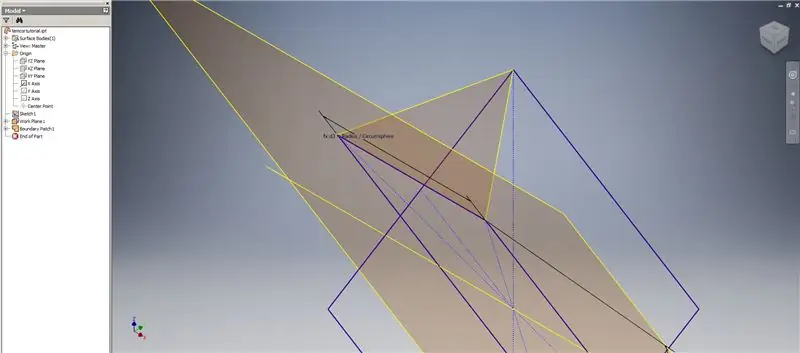
Nyní, když máme veškerou potřebnou geometrii, vytvořte ohraničující záplatu na druhém obrázku pomocí jakékoli metody, kterou upřednostňujete. Rozhodl jsem se udělat 3D skicu, ale skicování na jiné pracovní rovině by fungovalo stejně dobře.

Krok 5: Vytvoření křižovatkových rovin

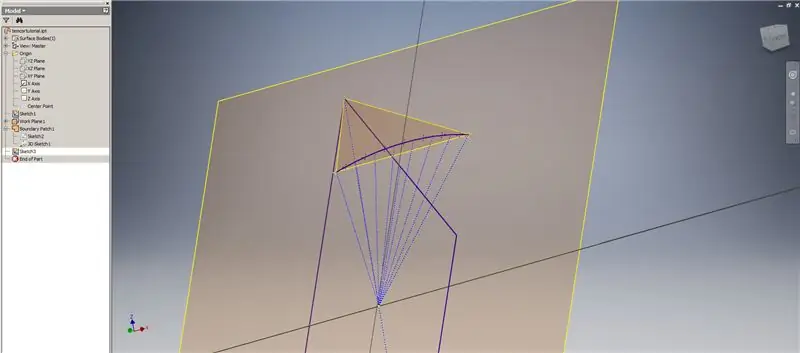
Začněte další skicu na první pracovní rovině („Pracovní rovina 1“), kterou jste vytvořili, promítněte rohy obdélníku Golden², poté spojte tyto body a počátek a vytvořte středový úhel 2v triacontahedronu. Vydělte to polovinou frekvence kopule, jako byste začínali rozpisem Metoda 2. Umístěte body na středy akordů.

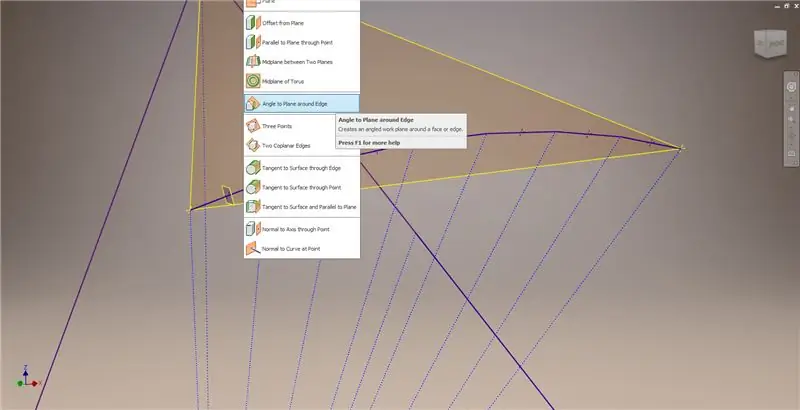
Ukončete skicu a vytvořte rovinu pomocí jednoho z akordů a jeho středu, jak ukazuje druhý obrázek. Poté vytvořte další pracovní rovinu pomocí „Úhel k rovině kolem okraje“. Vyberte pracovní rovinu 1 a jednu z konstrukčních čar zobrazenou na obrázku vpravo dole a vlevo dole. Přijměte výchozí úhel 90 stupňů, jinak by zbytek rozdělení nevypadalo správně. Opakujte postup pomocí zbývajících akordů a konstrukčních čar, abyste získali výsledek na obrázku vpravo dole.

Krok 6: Vytvoření křivek průsečíků a vytvoření podskupiny

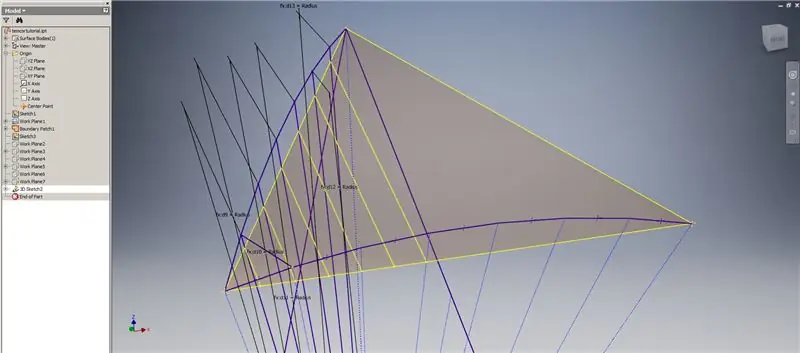
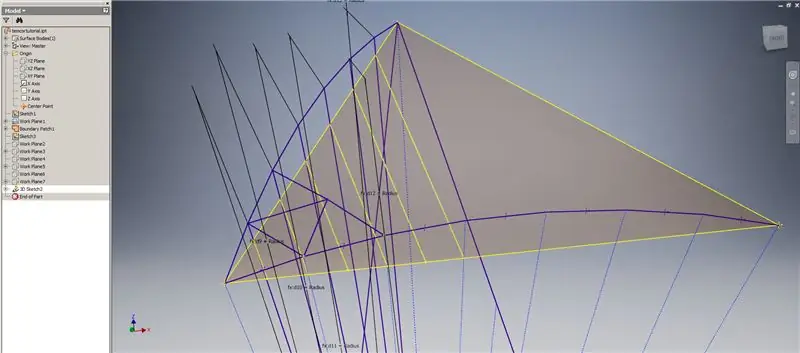
Spusťte 3D skicu a poté vytvořte průsečíkové křivky pomocí pracovních rovin, které jste právě vytvořili, a ohraničující záplaty, tvořící čáry zobrazené na horním obrázku.

Nakreslete čáry shodné s koncovými body křivek průsečíků, jak ukazuje obrázek 2. Srovnejte je všechny s poloměrem kopule. Nakreslete akordy spojující čáry, které leží na křivkách průsečíků. Připojte libovolnou geometrii, která vypadá dostatečně blízko, aby vytvořil trojúhelník dělení. Podívejte se na následujících 10 obrázků, u nichž se akordy zrcadlí napříč rovinami pracovních křižovatek - dokážou to vysvětlit lépe, než pouhá slova.

Krok 7: Dokončení kopule

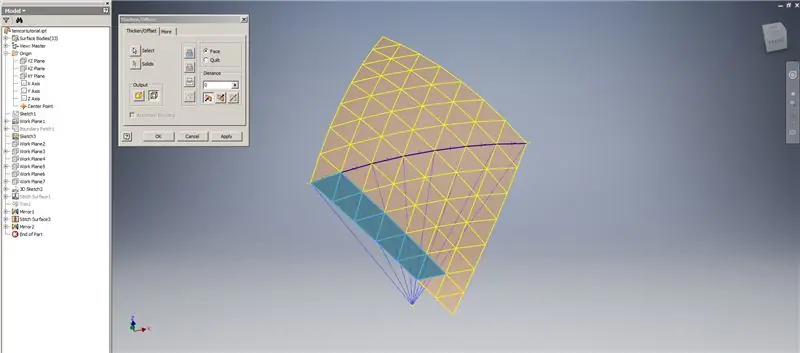
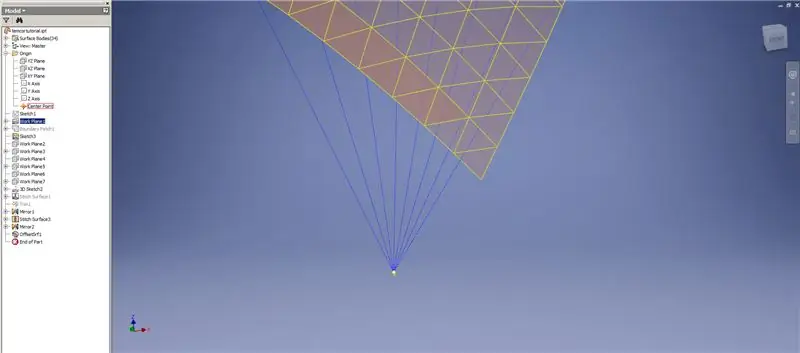
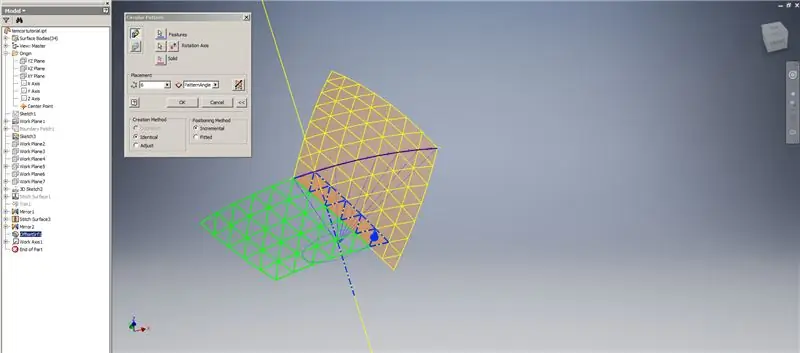
Vytvořte zesílení/odsazení spodních řádků, přičemž vynechejte poslední dvě řady trojúhelníků. Vzorujte nový OffsetSrf 6krát, nebo ((Frekvence = 14)/2) -1. Skrýt OffsetSrf, sešít vzorované povrchy a poté zrcadlit sešitý povrch pomocí roviny YZ. Vytvořte pracovní roviny spočívající na vrcholech horního trojúhelníku, jak je znázorněno na obrázku 6. Ořízněte prošité a zrcadlené povrchy pomocí těchto nových pracovních rovin a poté zbývající plochy sešijte k sobě. Vzorujte tento poslední povrch přes osu Z, poté sešijte tyto konečné povrchy k sobě a máte hotovo!

Krok 8: Kontrola akordů

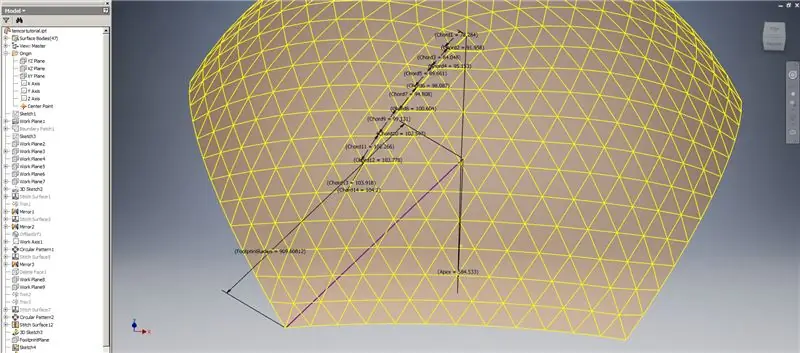
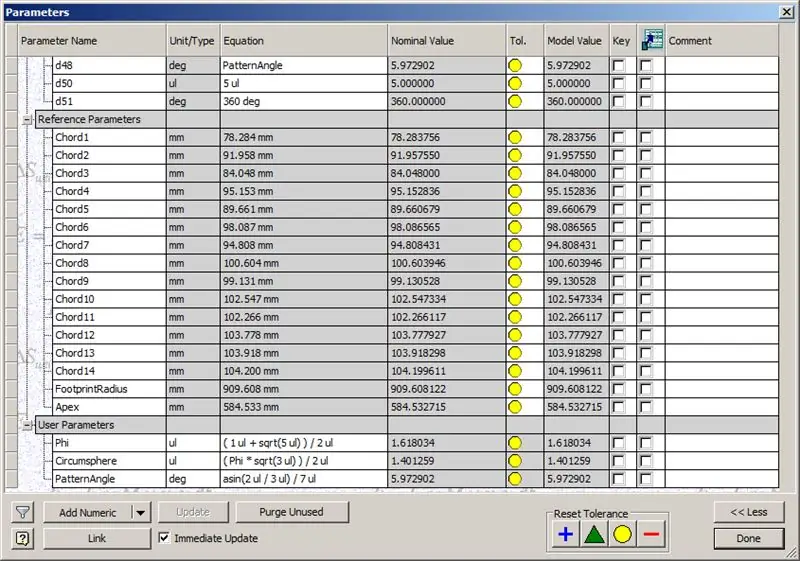
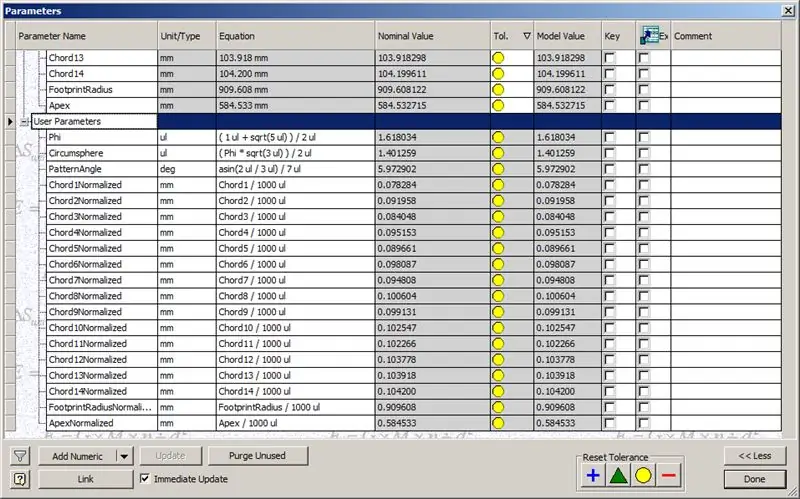
Naše kopule je tedy hotová, ale podívejme se, jestli se čísla shodují s modelem TaffGocha:

Pokud jde o referenční parametry, vypadá to, že se perfektně shodují!

Při rozdělení délek akordů o 1000 můžeme jasně vidět dokonalou korespondenci s akordovými faktory TaffGochova modelu, stejně jako s poloměrem stopy a vrcholovými faktory.