Měření teploty z PT100 pomocí Arduina: 6 kroků (s obrázky)

2024 Autor: John Day | [email protected]. Naposledy změněno: 2024-01-31 10:18

PT100 je odporový teplotní detektor (RTD), který mění svůj odpor v závislosti na okolní teplotě, je široce používán pro průmyslové procesy s pomalou dynamikou a relativně širokými teplotními rozsahy. Používá se pro pomalé dynamické procesy, protože RTD mají pomalé časy odezvy (o kterých mluvím více později), ale jsou přesné a mají malý posun v čase. To, co vám ukážu v tomto Instructable, by neodpovídalo průmyslovým standardům, ale vystaví vás alternativnímu způsobu měření teploty než pomocí LM35, s nímž by mnoho fandů bylo obeznámeno a ukázala teorii obvodů lze použít na jiné senzory.

Krok 1: Součásti

1x PT100 (dvouvodičový)

1x Arduino (libovolný model)

3x 741 provozních zesilovačů (LM741 nebo UA741)

1x odpor 80 ohmů

2x 3,9 kohmové odpory

2x 3,3 kohmové odpory

2x 8,2 kohmové odpory

2x 47kohms odpory

1x 5kohms potenciometr

1x Dva koncový napájecí zdroj nebo 8x 1,5V AA baterie

Používám dvouvodičový PT100, tří a čtyřvodičový PT100 budou mít různé obvody. Hodnoty odporů pro většinu z nich nemusí být úplně stejné jako výše, ale pokud existuje pár odporů, tj. 3,9 kohmů, pokud jste je vyměnili za řekněme 5k, budete muset vyměnit oba za 5k jako tehdy musí být stejný. Až získáme obvod, řeknu efekt výběru různých hodnot. Pro operační zesilovače (operační zesilovače) můžete použít jiné operační zesilovače, ale ty jsem použil.

Krok 2: Wheatstone Bridge

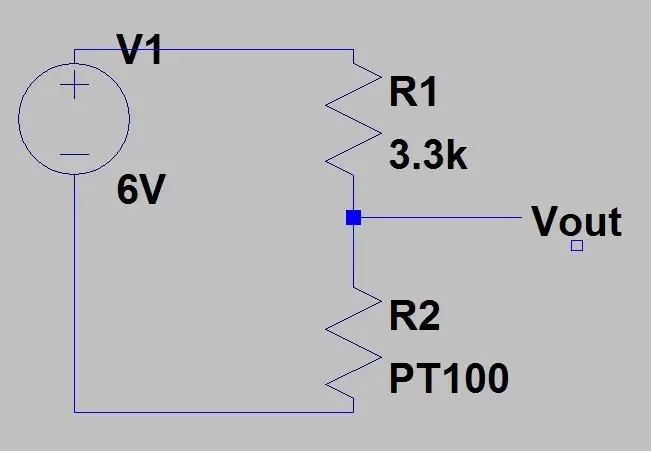
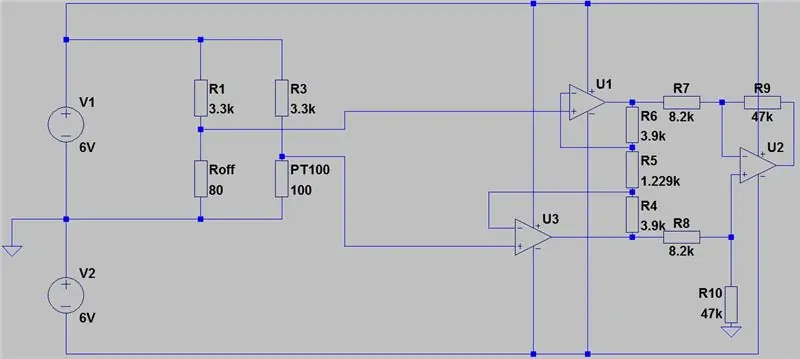
Nejprve musím mluvit o vzorci pro získání teploty z odporu pro PT100, než budu mluvit o první části obvodu, vzorec pro odpor je následující:

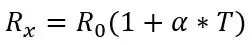
kde Rx je odpor PT100, R0 je odpor PT100 při 0 stupních C, α je koeficient teplotní odolnosti a T je teplota.

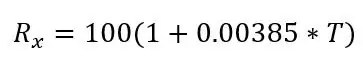
R0 je 100 ohmů, protože toto je PT100, kdyby to bylo PT1000, R0 by bylo 1000 ohmů. α je 0,00385 ohmů/stupňů C převzato z datového listu. K dispozici je také přesnější vzorec, který zde najdete, ale výše uvedený vzorec bude pro tento projekt stačit. Pokud transponujeme vzorec, můžeme vypočítat teplotu pro daný odpor:

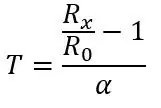
Řekněme, že chceme změřit něco, co by mělo teplotní rozsah -51,85 až 130 stupňů C, a umístili jsme PT100 do obvodu zobrazeného na obrázku 1. Pomocí výše uvedené rovnice a rovnice napětí z děliče napětí (zobrazeno na obrázku) na prvním obrázku) můžeme vypočítat rozsah napětí. Dolní část rozsahu T = -51,85 (80 ohmů)

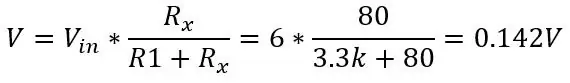
a při 130 stupních (150 ohmů):

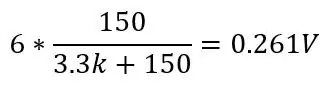
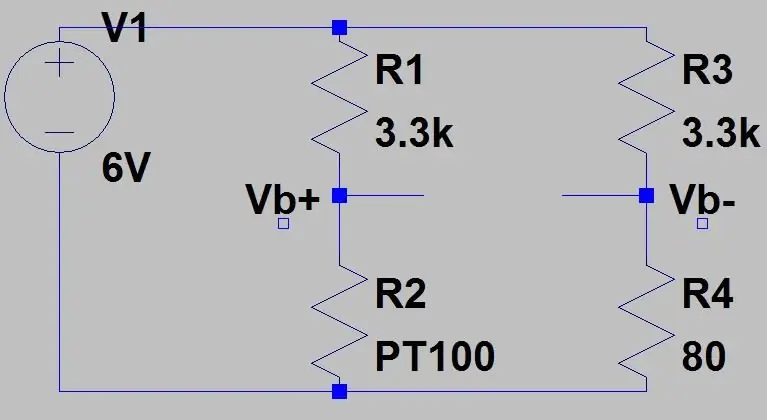
To by poskytlo rozsah 0,1187 V a DC offset 0,142, protože víme, že naše teplota se nikdy nedostane pod -51,85 ° C, což sníží citlivost v rozsahu, který nás zajímá (80 až 130 ohmů), když toto napětí zesílíme. Abychom se zbavili tohoto DC offsetu a zvýšili naši citlivost, můžeme použít Wheatstoneův můstek, který je ukázán na druhém obrázku.

Výstup druhého děliče napětí (Vb-) bude později odečten od výstupu prvního děliče napětí (Vb+) pomocí diferenciálního zesilovače. Vzorec pro výstup můstku jsou pouze dva děliče napětí:

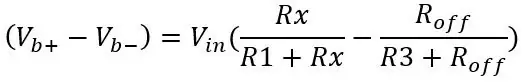
Napětí na PT100 je 80 ohmů a při použití dalších hodnot na obrázku:

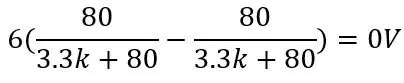
a pro Pt100 je 150 ohmů:

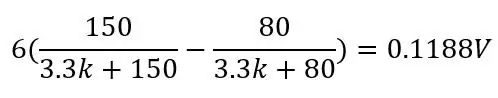
Použitím Wheatstone se zbavíme DC offsetu a zvýšíme citlivost po zesílení. Nyní, když víme, jak funguje Wheatstoneův most, můžeme mluvit o tom, proč používáme 80 ohmů a 3,3 kohmů. 80 ohmů je druh vysvětlen z výše uvedeného vzorce, zvolte tuto hodnotu (budeme tomu říkat ofsetový odpor Roff) jako spodní rozsah vaší teploty nebo ještě lépe, mírně pod spodkem vašeho rozsahu, pokud se používá pro řídicí systémy pro regulaci teploty nebo něco podobného, chtěli byste vědět, jak nízko se teplota dostává pod váš teplotní rozsah. Pokud je tedy -51,85 ° C spodní část vašeho rozsahu, použijte pro Roff 74,975 ohmů (-65 stupňů C).

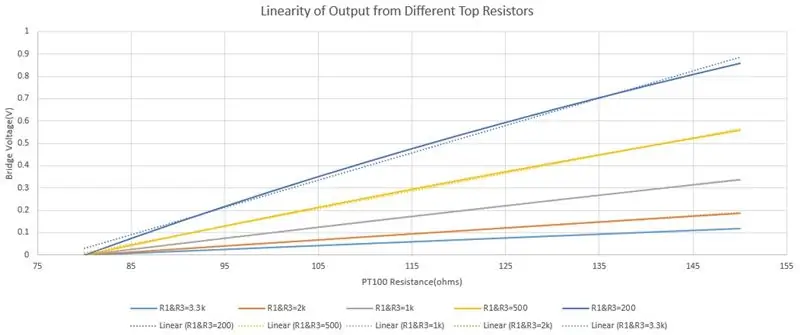
3.3k pro R1 a R3 jsem zvolil ze dvou důvodů, kvůli omezení proudu a zvýšení linearity výstupu. Protože PT100 mění odpor v důsledku teploty, průchod příliš velkého množství proudu způsobí nesprávné hodnoty kvůli samovolnému zahřívání, takže jsem zvolil maximální proud 5-10mA. Když je PT100 80 ohmů, proud je 1,775 mA, takže bezpečně pod maximálním rozsahem. Snížíte odpor, abyste zvýšili citlivost, ale to by mohlo mít negativní vliv na linearitu, protože budeme používat rovnici čáry později (y = mx+c) s nelineárním výstupem způsobí chyby. Na třetím obrázku je graf výstupu můstku pomocí různých horních odporů, plná čára je skutečný výstup a tečkovaná čára je lineární aproximace. V tmavě modrém grafu (R1 a R3 = 200 ohmů) vidíte, že poskytuje největší rozsah napětí, ale výstup je nejméně lineární. Světle modrá (R1 a R3 = 3,3 kohms) poskytuje nejmenší rozsah napětí, ale tečkovaná čára a plná čára se překrývají, což ukazuje, že její linearita je velmi dobrá.

Nebojte se změnit tyto hodnoty tak, aby vyhovovaly vaší aplikaci, také pokud změníte napětí, zajistěte, aby proud nebyl příliš vysoký.

Krok 3: Zesílení

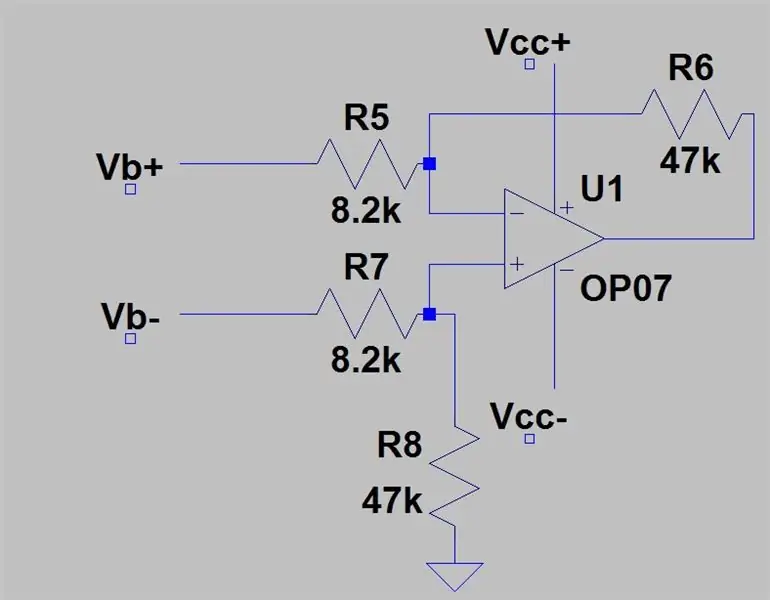
V posledním kroku jsme zjistili, že výstupní rozsah dvou odečtených děličů napětí byl 0 až 0,1187, ale nemluvili jsme o tom, jak tato napětí odečíst. K tomu budeme potřebovat diferenciální zesilovač, který odečte jeden vstup od druhého a zesílí to ziskem zesilovače. Obvod pro diferenciální zesilovač je zobrazen na prvním obrázku. Nakrmíte Vb+ do invertujícího vstupu a Vb- v neinvertujícím vstupu a výstupem bude Vb+- Vb- se ziskem jednoho, tj. Bez zesílení, ale přidáním odporů zobrazených na obrázku přidáme zisk 5,731. Zisk je dán:

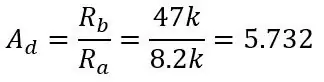
Ra je R5 a R7 a Rb je R6 a R8, výstupní napětí je dáno vztahem:

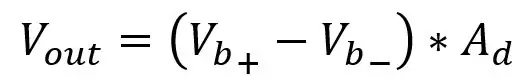
Existují jen dva problémy s připojením tohoto zesilovače k výstupu můstku, efekt načítání a změna zisku. Změna zisku zesilovače vyžaduje, abyste změnili alespoň dva rezistory, protože dva páry rezistorů musí být stejné, takže mít dva hrnce, které musí mít stejnou hodnotu, by bylo nepříjemné, takže použijeme něco, čemu se říká přístrojový zesilovač o kterém mluvím níže. Efekt zatížení je, že vstupní rezistory do zesilovače ovlivňují pokles napětí na PT100, chceme, aby napětí na PT100 bylo nezměněno, a abychom to mohli udělat, můžeme pro vstupní rezistory zvolit velmi velké rezistory tak, aby paralelní odpor PT100 a vstupní odpor je velmi blízko odporu PT100, ale to může způsobit problémy s posunem šumu a výstupního napětí, do kterého se nechystám. Stačí vybrat střední rozsah v rozmezí Kohms, ale jak jsem říkal, mít malé odpory je také špatné, takže trochu změníme obvod.

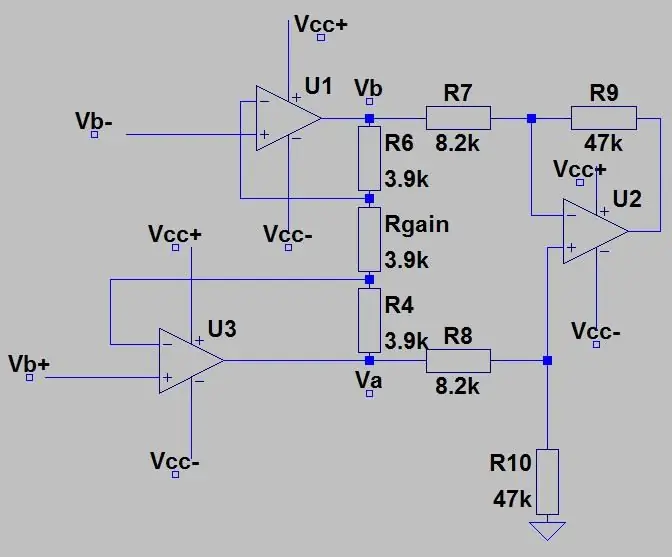
Na druhém obrázku máme výstup můstku připojený k přístrojovému zesilovači, který působí jako vyrovnávací zesilovač pro oddělení dvou polovin obvodů (můstek a zesílení) a také umožňuje použití pro zesílení vstupu změnou pouze jednoho potenciometru (Rgain). Zisk přístrojového zesilovače je dán:

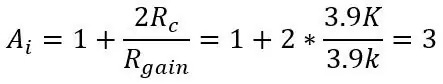
kde Rc jsou dva rezistory 3,9k nad a pod potem.

Snížením Rgain se zesílení zvyšuje. Pak v bodě Va a Vb (zesílené Vb+ a Vb-) je to jen diferenciální zesilovač jako dříve a celkový zisk obvodu jsou jen zisky vynásobené dohromady.

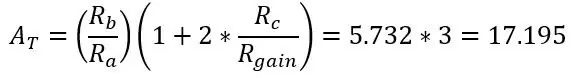
Chcete -li zvolit svůj zisk, který chcete udělat něco jako předtím s Roffem, měli bychom vybrat odpor těsně nad vaší maximální teplotou ve vašem rozsahu pro případ, že by došlo k jeho překročení. Protože používáme Arduino, které má 5V adc, maximální výkon obvodu by měl být 5V při maximální teplotě, kterou jste si vybrali. Vyberme 150 ohmů, protože maximální odpor a nezesílené napětí můstku bylo 0,1187 V, potřebný zisk je 42,185 (5/0,1187)

Řekněme, že ponecháme Ra, Rb a Rc jako 8,2k, 47k a 3,9k, stačí najít hodnotu pro pot Rgain:

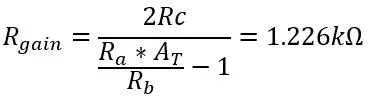
Abyste dostali všech 5 voltů z používaného teplotního rozsahu, změňte hodnotu Rgain na 1,226 k. Výstupní napětí vycházející z diferenciálního zesilovače je dáno vztahem:

Krok 4: Napájení obvodu

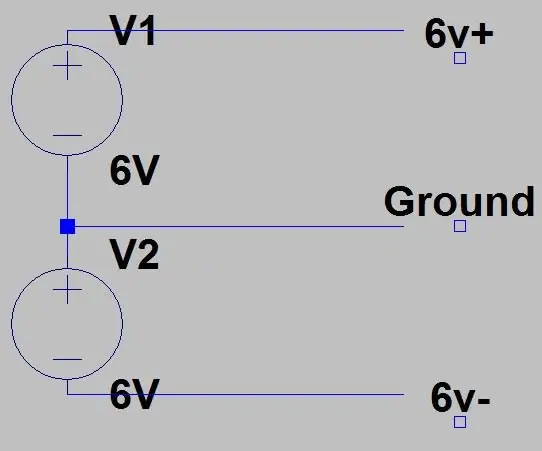
Toto je poslední krok obvodu, možná jste si všimli Vcc+ a Vcc- na obvodech operačního zesilovače, protože pro správnou funkci potřebují kladné i záporné napětí, můžete získat jednokolejné operační zesilovače, ale rozhodl jsem se používat tento zesilovač, protože to je to, co jsem ležel kolem. Budeme tedy dodávat +6V a -6V, existují tři způsoby, jak to udělat. První je zobrazen na prvním obrázku, kde musíme dva napájecí zdroje nebo dva výstupní terminály z jednoho napájecího zdroje, mít oba na 6 V a mít jeden kladný výstup připojený k záporu druhého. 6V horního napájení bude našich +6V, kladné spodní napájení je GND a záporné spodní napájení je -6V. PŘIPOJTE JEN TAK, TAK, KDYŽ JSOU ODDĚLENY GNDY DVĚCH ZDROJŮ NEBO POŠKOZÍ VAŠE NAPÁJENÍ. Všechny komerční napájecí zdroje by měly oddělené GND, ale pokud to chcete zkontrolovat, použijte na multimetru tester kontinuity, pokud bzučí, toto nastavení nepoužívejte a použijte další. Na své domácí dodávce jsem přepálil pojistku.

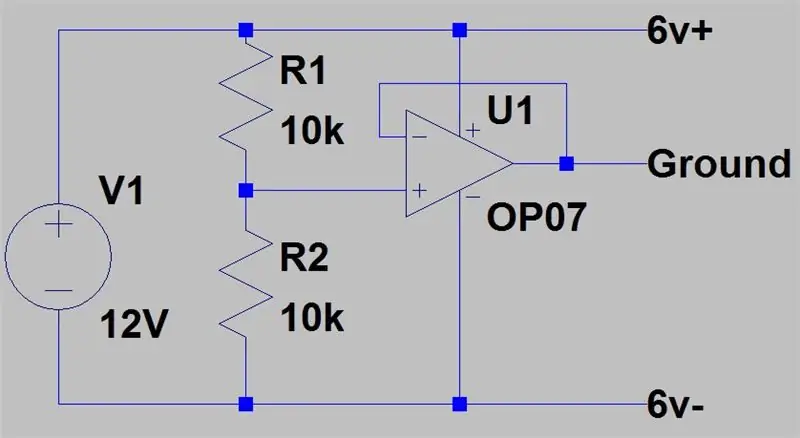
Na druhém obrázku je druhé nastavení, které můžeme mít, vyžaduje, aby jeden zdroj měl dvojnásobné napětí než ostatní, ale nepoškodí napájení, pokud jsou připojeny GND. Máme dva zdroje, jeden na 12V a druhý na 6V. 12V bude fungovat jako našich +6V, 6V z druhého zdroje bude fungovat jako GND a dva skutečné GND ze zdrojů budou fungovat jako -6V.

Toto poslední nastavení je pro napájecí zdroje s pouze jedním výstupem, používá vyrovnávací zesilovač se ziskem 1 k vytvoření virtuální země průchodem poloviny napájecího napětí přes vyrovnávací zesilovač. Poté bude 12V fungovat jako +6V a skutečný terminál GND bude -6V.

Pokud chcete používat baterie, doporučil bych první nastavení, ale problém s bateriemi spočívá v tom, že napětí začne klesat, když začnou odumírat, a napětí na můstku také klesne, což způsobí nesprávné odečty teploty. Napětí z baterií jste samozřejmě mohli přečíst a zahrnout je do výpočtů nebo použít regulátory a další baterie. Nakonec je to na vás.

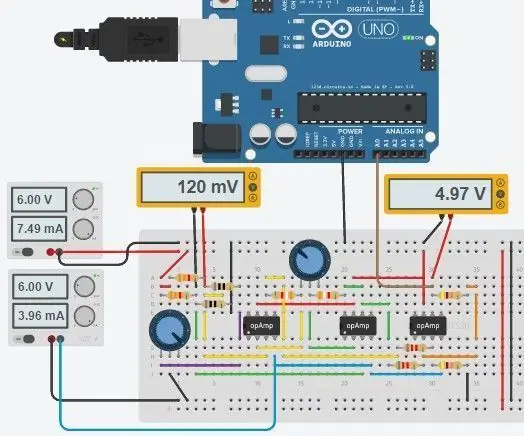
Krok 5: Úplný obvod a kód

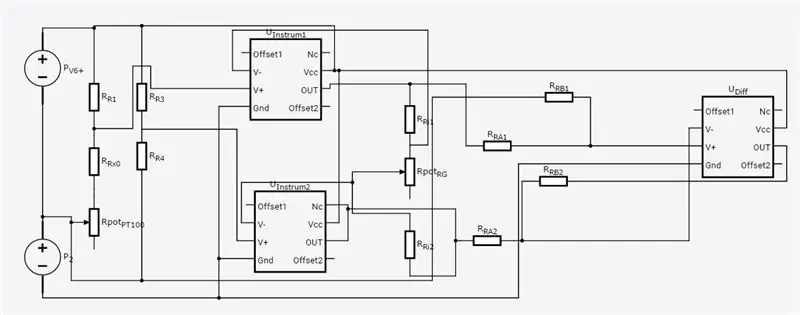
Celý obvod je zobrazen výše a byl vytvořen v novém Circuits.io společnosti Autodesk, který vám umožňuje vytvářet obvody na breadboardu, upravovat schéma zapojení (viz obrázek 2) a diagramy plošných spojů a nejlepší část, umožňuje simulovat obvod z prkénka a můžete dokonce naprogramovat Arduino a připojit jej v režimu breadboard, dále na stránce je simulace a můžete si hrát se dvěma poty. Pokud chcete obvod duplikovat a zadat své vlastní hodnoty, najdete zde obvod. První potenciometr je 70 ohmů a v sérii s odporem 80 ohmů, který simuluje PT100 s rozsahem 80-150 ohmů, druhý potenciometr je zisk zesilovače instrumentace. Bohužel jsem pro svůj kód použil knihovnu, kterou jsem stáhl, takže Arduino není zahrnuto v níže uvedeném obvodu, ale k připojení potřebujete pouze dva další vodiče. Pokud vám více vyhovuje LTspice, přidal jsem do obvodu soubor asc.

Připojte pin A0 k výstupu diferenciálního zesilovače

Připojte GND Arduina k GND obvodu (NE -6V)

A tím je obvod hotový, nyní ke kódu. Dříve jsem zmínil, že použijeme vzorec y = mx+c, nyní tedy budeme počítat m (sklon) a c (offset). V Arduinu budeme číst napětí, ale teplotní rovnice potřebuje, abychom znali odpor PT100, takže způsob, jak to můžeme udělat, je nahradit Serial.println (temp) Serial.println (V) a zaznamenat napětí a odporu při dvou teplotách. Při tomto testu nechte PT100 na chvíli, třeba minutu nebo dvě, v klidu a držte se mimo dosah jakýchkoli zdrojů tepla (sluneční světlo, ventilátor notebooku, vaše tělo atd.).

První bod, který můžeme vzít, je pokojová teplota, když máte zapojený a funkční obvod, zaznamenejte napětí (Vt1) načtené Arduinem na sériovém monitoru a rychle odpojte PT100 a zaznamenejte jeho odpor (Rt1), nedávejte ruce na sondu při odpojování, protože to změní odpor. Pro druhou teplotu bychom mohli sondu umístit do ledové vody nebo horké vody (při použití horké vody buďte opatrní) a zopakujte to, co jsme udělali, než jsme našli Vt2 a Rt2. Hned po vložení sondy do kapaliny počkejte minutu nebo dvě, než se odpor ustálí. Pokud vás zajímá časová odezva PT100, zaznamenejte napětí ze sériového monitoru přibližně každé 2 sekundy a můžeme z toho nakreslit graf a vysvětlím to později. Pomocí dvou napětí a odporů můžeme vypočítat sklon následujícím způsobem:

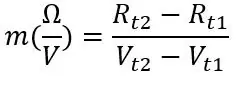
Rt1 a Rt2 jsou odpory při těchto dvou teplotách a platí to i pro napětí Vt1 a Vt2. Ze sklonu a jedné ze dvou sad bodů, které jste zaznamenali, můžeme vypočítat posun:

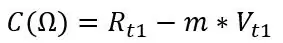
C by mělo být blízké vašemu skutečnému Roffovi, ze své simulace jsem vypočítal tyto hodnoty:

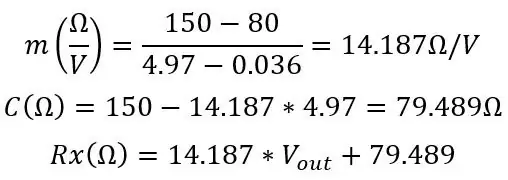
Z tohoto odporu můžeme zjistit naši teplotu pomocí vzorce, který jsme měli na začátku:

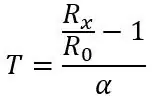
A je to, kód pro Arduino je níže, pokud máte nějaké problémy, stačí zanechat komentář a pokusím se pomoci.

Nejsou k dispozici žádné obrázky obvodu, který jsem vytvořil před chvílí, a už nemám PT100 k předělání a testování, ale musíte mi věřit, že to funguje. Nenašel jsem mnoho o PT100 na Instructables, takže jsem to udělal ible.

V dalším kroku budu hovořit o časové odezvě PT100 a pokud vás nezajímá matematika, když měříte změnu teploty, nechte PT100 na minutu usadit, než začnete číst.

Pokud máte zájem vidět další projekty, které jsem vytvořil, navštivte mé

Blog: Roboroblog

Kanál YouTube: Roboro

Nebo se podívejte na mé další Instructables: zde

Pokud si HTML poradí s níže uvedeným kódem, je kód připojen

* Tento kód vypočítává teplotu pomocí PT100

* Napsal Roboro * Github: <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… <a href =" https://github.com/RonanB96/Read-Temp- From-PT100-… <a href = "https://github.com/RonanB96/Read-Temp-From-PT100-… >>>>>>>>> * Circuit: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Blog: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * Instrustable Post: <a href=" href="https://github.com/RonanB96/Read-Temp-From-PT100-… <a href=" https://github.com/ronanb96/read-temp-from-pt100-…="">>>>>>>>>> * */ //You'll need to download this timer library from here //https://www.doctormonk.com/search?q=timer #include "Timer.h" // Define Variables float V; float temp; float Rx; // Variables to convert voltage to resistance float C = 79.489; float slope = 14.187; // Variables to convert resistance to temp float R0 = 100.0; float alpha = 0.00385; int Vin = A0; // Vin is Analog Pin A0 Timer t; // Define Timer object

void setup() {

Serial.begin(9600); // Set Baudrate at 9600 pinMode(Vin, INPUT); // Make Vin Input t.every(100, takeReading); // Take Reading Every 100ms } void loop() { t.update(); // Update Timer } void takeReading(){ // Bits to Voltage V = (analogRead(Vin)/1023.0)*5.0; // (bits/2^n-1)*Vmax // Voltage to resistance Rx = V*slope+C; //y=mx+c // Resistance to Temperature temp= (Rx/R0-1.0)/alpha; // from Rx = R0(1+alpha*X) // Uncommect to convet celsius to fehrenheit // temp = temp*1.8+32; Serial.println(temp); }

Step 6: Time Response of PT100

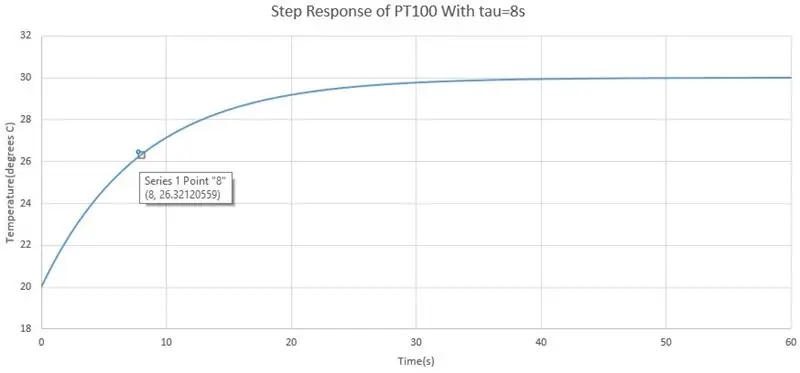
Zmínil jsem tedy, že PT100 má pomalou odezvu, ale můžeme získat vzorec pro aktuální teplotu načtenou PT100 kdykoli t. Odpověď PT100 je odpovědí prvního řádu, kterou lze zapsat Laplaceovým výrazem, tj. Přenosovou funkcí, jako:

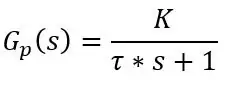
kde tau (τ) je časová konstanta, K je zisk systému a s je Laplaceův operátor, který lze zapsat jako jω, kde ω je frekvence.

Časová konstanta vám řekne, jak dlouho trvá, než se systém prvního řádu ustálí na své nové hodnotě. Pravidlem nebo pravidlem je, že 5*tau je doba, po kterou se ustálí v novém ustáleném stavu. Zisk K vám řekne, jak moc bude vstup zesílen. U PT100 je zisk to, jak moc se odpor mění děleno změnou teploty, z výběru dvou náhodných hodnot z tohoto datového listu jsem získal zisk 0,3856 ohm/C.

Než jsem řekl, můžete zaznamenávat napětí každé 2 s poté, co jste sondu vložili do kapaliny, horké nebo studené, z toho můžeme vypočítat časovou konstantu systému. Nejprve musíte určit, kde je počáteční bod a koncový bod, počátečním bodem je napětí, než vložíte sondu do kapaliny a koncový bod, když se usadí. Poté je odečtěte a to je změna napětí kroku, test, který jste provedli, byl skokovou změnou, což je náhlá změna vstupu do systému, přičemž krokem je teplota. Nyní v grafu přejděte na 63,2% změny napětí a tato doba je časová konstanta.

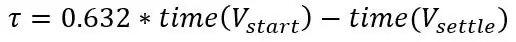
Pokud tuto hodnotu zapojíte do přenosové funkce, budete mít vzorec pro popis frekvenční odezvy systémů, ale to není to, co chceme právě teď, chceme skutečnou teplotu v čase t pro teplotní krok, takže jdeme muset provést inverzní Laplaceovu transformaci kroku do systému. Přenosová funkce systému prvního řádu se zadáním kroku je následující:

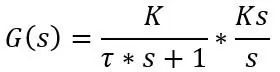
Kde Ks je velikost kroku, tj. Teplotní rozdíl. Řekněme, že sonda je usazena při 20 stupních C, umístěna do vody při 30 stupních C a sonda má časovou konstantu 8 s, přenosová funkce a vzorec časové domény je následující:

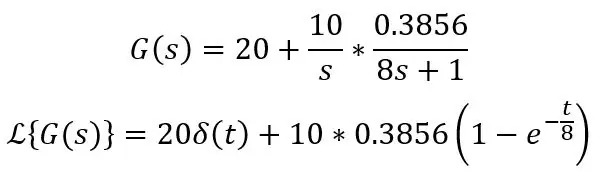
Δ (t) v tomto případě znamená impuls, tj. DC offset o 20 stupňů C, při výpočtu můžete do svých rovnic napsat pouze 20. Toto je standardní rovnice pro krok do systému prvního řádu:

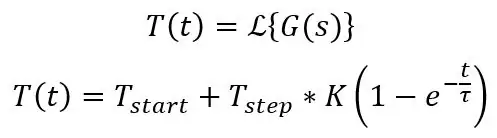
Výše uvedené vypočítá teplotu v čase t, ale to bude fungovat pro napětí, protože jsou navzájem úměrné, potřebujete pouze počáteční a koncovou hodnotu, časovou konstantu a velikost kroku. Web s názvem Symbolab je skvělý ke kontrole, zda je vaše matematika správná, dokáže Laplaceovu, integrační, diferenciační a spoustu dalších věcí a poskytuje vám všechny kroky na cestě. Inverzní Laplaceovu transformaci výše uvedeného naleznete zde.