Včasné varování Raspberry PI Runway Light using Flight Mapping Data: 14 Steps (with Pictures)

2024 Autor: John Day | [email protected]. Naposledy změněno: 2024-01-30 08:21

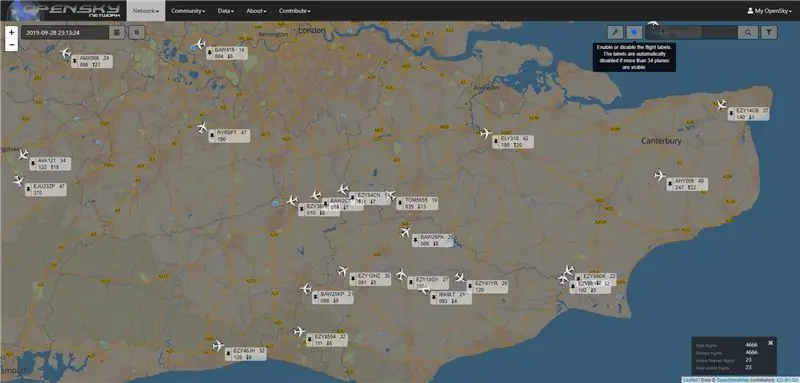
Tato lampa vznikla z několika důvodů v tom, že mě vždy zajímají letadla, která létají nad hlavou, a v létě o víkendech často létají docela vzrušující. I když je jen slyšíte, když jdou kolem. Dalším důvodem je to, že se zdá, že letová trasa odchozích letadel z letiště London City bude někdy zaslechnuta a budou mít docela hlučné lety. Jelikož jsem se pustil do nahrávání některých videí na YouTube, je opravdu otravné muset záznam zrušit kvůli hlučnému letadlu. Zajímalo mě tedy, zda jsou data, která vidíte na stránkách, jako je flightradar24, veřejně dostupná, jakmile jsem zjistil, že něco podobného je dostupné z opensky sítě, zrodila se lampa včasného varování. Netrvalo dlouho a pak přišel nápad použít k umístění projektu repliku dráhy.

Více informací o síti OpenSky najdete na https://www.opensky-network.org Také jsem tentokrát chtěl místo použití průsvitné PLA vyrobit pěknou pryskyřičnou čočku a přestože mám přijímač ADS-B, chtěl jsem si ji ponechat takhle jednoduché a levné. ADS-B také potřebuje anténu a to by neudělalo, aby lampa šla na polici v kanceláři. Doufejme tedy, že vás stavba zaujme, protože pokrývá 3D tisk, tvarování pryskyřice a matematiku a také extrapolaci pozic letadel, která by potenciálně mohla letět nad hlavou.

Krok 1: Navrhování pouzdra

Vyhledávání Google přichází s mnoha různými návrhy lamp na přistávací dráhu a design této byl vytvořen pomocí designových vlivů z mnoha různých značek skutečných lamp. Je také přizpůsobeno spíše sedět v místnosti nebo na polici než v plné velikosti, protože v reálném životě bývají mnohem větší.

Návrhy byly zpracovány ve Fusion 360 a já jsem importoval některé předchozí prvky, jako je držák nulového malinového pi z předchozích projektů. Schopnost znovu použít prvky vyžaduje spoustu bolesti hlavy, aby se nedostaly základy. Soubory si také můžete stáhnout zde

Krok 2: Lití čoček - #fail

Nejdůležitějším designovým prvkem této lampy měl být objektiv. Nejprve jsem to tedy vyřešil, protože bez hezkého autentického skla by projekt fungoval. Zdokumentuji zde neúspěchy, kterých jsem se pokusil dosáhnout, bez ohledu na to, že jsem se také původně rozhodl udělat čočku jantarovou. Dráhová světla přicházejí v oranžové i modré barvě a teprve poté, co jsem začal vyrábět jantarové, jsem si to rozmyslel a rozhodl jsem se, že chci modré.

Z toho, co mohu zjistit, jantarové se používají na přídržné lince a modré se používají k lemování dráhy, a to jsou ty, které se zdají být archetypálnějšími, které najdete, pokud hledáte světla dráhy. Zde je však můj první pokus o výrobu jantarové čočky. K výrobě čočky jsem použil čirou litou pryskyřici s barevnou přísadou, a přestože jsem udělal několik forem, než jsem přemýšlel, jestli bude možné vytisknout 3D formu a použít ji. Začal jsem tedy dělat dělenou formu ve 3D a vytisknout ji v PetG. Byl jsem přesvědčen, že rozumné množství uvolňování plísní by stačilo na roztroušení formy. Jak se ukázalo při několika pokusech, pryskyřici jsem přilepil k formě jako lepidlo a nezdálo se možné je oddělit. Ačkoli jsem měl ten plný, který jsem chtěl použít, rozhodl jsem se proti tomu a vytiskl jsem objektiv pro použití s tradičním silikonovým tvarováním.

Krok 3: Různé druhy pryskyřice

Jako rychlou stranou jsem pro tento projekt použil 3 typy čirých/barevných pryskyřic.

První byl Hobby market s názvem Pebeo - Gedeo a běžně se prodává na zapouzdření drobných předmětů a používá se na šperky a stolní těžítka atd. To fungovalo docela dobře a pěkně se to vyléčilo asi za 24–36 hodin. Je to však docela drahé za částku, kterou získáte, ale je praktické a snadno dostupné v hobby a řemeslných obchodech. Je smíchán v poměru 2: 1. Druhou byla předbarvená pryskyřice, která se smíchá v poměru 10: 1 s tužidlem a její vytvrzení trvalo nejdéle, asi týden, abych byl upřímný, než se úplně vytvrdila. Poslední byla čirá pryskyřice, která byla také smíchána v poměru 2: 1 a která byla vytvrzena asi za 2 dny, můžete ji obarvit kapkami pigmentu, ale musíte zajistit, abyste vždy používali stejný poměr barev, pokud vyrábějí oddělené dávky. Funguje to také nákladově nejefektivnější. Nakonec RTV pro formu byla GP-3481 RTV a její nastavení trvá asi 24 hodin a má docela dlouhou dobu zpracovatelnosti, takže máte spoustu času ji promíchat a poté nalít.

V současné době nemám vakuový hrnec (v současné době na objednávku), takže vás mohou sužovat bubliny ve formě i v nalévání pryskyřice. Není to příliš problém, ale s čistým objektivem nebo podobným byste chtěli přemýšlet o tom, jak dostat bubliny ze směsí.

Krok 4: Lití objektivu do silikonové formy #2

Toto je tedy druhý pokus o výrobu resinové čočky a první fází bylo vyrobit jak čočku ve Fusion 360, tak ji vytisknout v ABS, stejně jako kbelík, který ji udrží. To by bylo první pro formu a pomáhá snížit množství použitého silikonu. Můžete to snadno vytvořit z karty, ale je to jen jiný přístup. Abych měl větší šanci, že se uvolní z formy, nejprve jsem ji nalakoval a poté jí dobře pokryl prostředek uvolňující vosk.

Poté jsem nalil trochu GP-3481, což je asi břeh 27 RTV, a pak jsem nechal nastavit dalších 24 hodin před odformováním. Jakmile to bylo hotovo, použil jsem čirou pryskyřici smíchanou v poměru 2: 1 s asi 4/5 kapkami barevného pigmentu a dobře míchal dobré čtyři minuty. Nalilo to do formy a poté se do pryskyřice také vložilo skleněné sklenice, aby se později vytvořila prázdnota pro lampu nebo LED diody. Asi po 24 hodinách byla tato pryskyřice připravena k odstranění a čočka vyšla docela dobře. Jsou tam vzduchové bubliny, ale zatím nemám vakuovou nádobu na odplynění pryskyřice před nalitím.

Krok 5: 3D tisk a příprava

Model byl navržen tak, aby se centrální část zasunula do základny. To mělo zabránit maskování během procesu malování. Celý model byl vytištěn v Hatchbox ABS a poté vybroušen. Počínaje zrnitostí 60 až zhruba 800 zrna poskytlo tomuto modelu dostatečně dobrou povrchovou úpravu.

Krok 6: Montáž a malování

Jakmile jsou výtisky vybroušeny, byly natřeny základním základním nátěrem. Lehce zbroušené a poté nastříkané šedým základním nátěrem. Hlavní části byly natřeny signální žlutou barvou Ford a poté jako základna použita brooklandská zeleň. na šrouby byly poté naneseny odstíny stříbra tamiya a na držák objektivu byl použit nějaký molotow stříbrný chrom.

Krok 7: Nejprve najděte letadla v ohraničující oblasti

S vytříděným hardwarem bylo potřeba na softwaru zapracovat. Nyní existuje několik webů, které poskytují sledování letů, ale jen málo z nich poskytuje API pro přístup k těmto datům. Někteří to dělají, pouze na komerční bázi, ale naštěstí existuje jeden web s názvem https://opensky-network.org, který můžete použít zdarma.

K přístupu k těmto datům se musíte zaregistrovat a poté můžete použít jejich API, které poskytuje několik funkcí a způsobů, jak data stáhnout. Máme zájem o všechny lety v rámci oblasti a mají k tomu volání Live API. https://opensky-network.org/apidoc/ se nazývá ohraničující rámeček. Volání API vyžaduje rohy pole, které vás zajímají, samozřejmě jako středový bod naši Lat/Lon. Můžete zkontrolovat matematické funkce tohoto webu, který nakreslí rámeček podle toho, co zadáte. “Http://tools.geofabrik.de, ale prozatím následující skript uvádí body, které potřebujeme zapojit do API.

funkce get_bounding_box ($ latitude_in_degrees, $ longitude_in_degrees, $ half_side_in_miles) {$ half_side_in_km = $ half_side_in_miles * 1,609344; $ lat = deg2rad ($ latitude_in_degrees); $ lon = deg2rad ($ longitude_in_degrees); $ radius = 6371; $ parallel_radius = $ radius*cos ($ lat); $ lat_min = $ lat - $ half_side_in_km/$ radius; $ lat_max = $ lat + $ half_side_in_km/$ radius; $ lon_min = $ lon - $ half_side_in_km/$ parallel_radius; $ lon_max = $ lon + $ half_side_in_km/$ parallel_radius; $ box_lat_min = rad2deg ($ lat_min); $ box_lon_min = rad2deg ($ lon_min); $ box_lat_max = rad2deg ($ lat_max); $ box_lon_max = rad2deg ($ lon_max); návratové pole ($ box_lat_min, $ box_lon_min, $ box_lat_max, $ box_lon_max);

Pokud chcete otestovat svůj kód, existuje web, kde můžete zadat lat/lon a zobrazit výsledky na mapě: Viz příklad ohraničovacího rámečku na mapě

Krok 8: Výpočet nadpisu letadel ve vztahu k nám

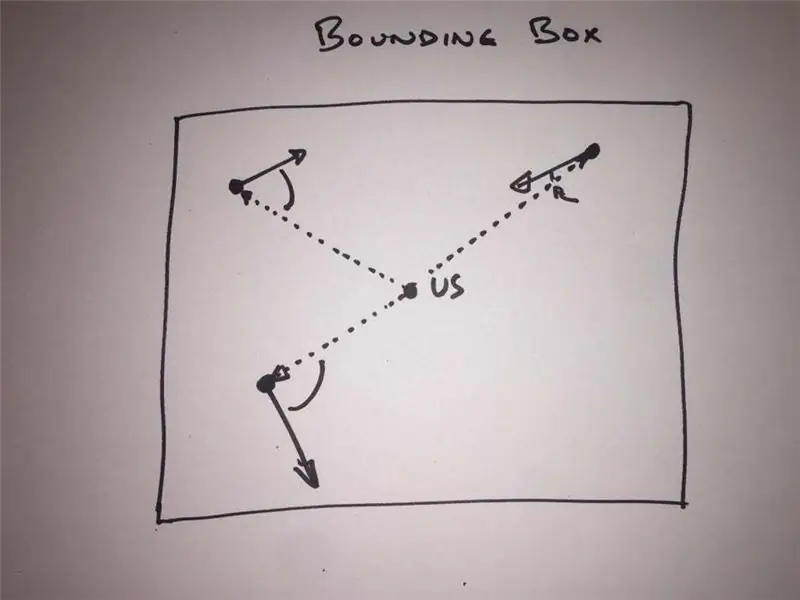
Výsledky z volání API ohraničujícího rámečku nám poskytnou seznam letadel, jejich Lon/lat, rychlost, nadmořskou výšku a směr. Další věc, kterou musíme udělat, je získat záhlaví každé roviny ve vztahu k nám, abychom mohli dále zpracovávat ty, které směřují alespoň naším obecným směrem. Můžeme to udělat, protože známe svou polohu a dokážeme vypočítat úhel od nás ke každé rovině.

K tomu používám kousek kódu, ze kterého byl původně Javascript, takže jsem ho zde převedl na PHP, * vypočítat (počáteční) směr mezi dvěma body * * od: Ed Williams 'Aviation Formulary, https://williams.best.vwh.net/avform.htm#Crs * source = instantglobe.com/CRANES/GeoCoordTool.html */ funkce get_bearing ($ home_lat, $ home_lon, $ plane_lat, $ plane_lon) {$ lat1 = deg2rad ($ home_lat); $ lat2 = deg2rad ($ plane_lat);

$ dLon = deg2rad ($ plane_lon- $ home_lon);

$ y = sin ($ dLon) * cos ($ lat2);

$ x = cos ($ lat1)*sin ($ lat2) - sin ($ lat1)*cos ($ lat2)*cos ($ dLon); $ z = atan2 ($ y, $ x); $ zz = (rad2deg ($ z) +360)% 360; vrátit $ zz;

Pokud se chcete podívat na stránku, kde jsou původní verze javascriptu, toto je odkaz:

v rámci tohoto kódu můžete také vidět různé dílčí rutiny pro každý typ výpočtu.

Krok 9: Výpočet zachycení pohledem na kruh

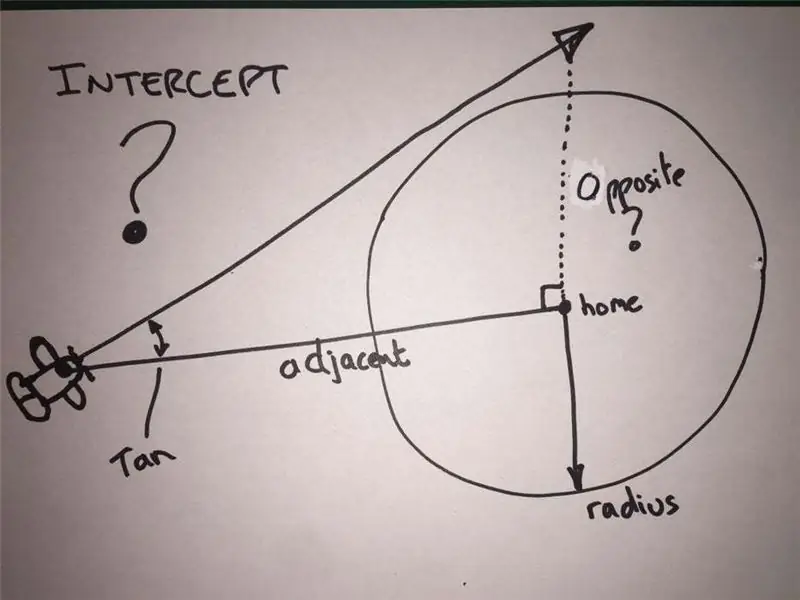
Nyní tedy máme letadlo, kde je ložisko mezi ním a naší polohou menší než 90 (pozitivní nebo negativní), a tak to znamená, že existuje šance, že by mohlo létat poblíž. Pomocí vzorce haversine můžeme také vypočítat pomocí Lon/Lat letadla a Lon/Lat našeho domu vzdálenost, která je od nás.

Když se podíváme na diagram, nakreslíme -li kruh kolem našeho domu, řekněme o poloměru 3 míle, máme šanci vidět, jak něco letí. Známe rozdíl v míření mezi letadlem a námi, známe také vzdálenost letadla od nás, abychom pak mohli vypracovat trojúhelník pomocí starého dobrého SOHCAHTOA a v tomto případě pomocí Tan úhlu můžeme získat délka opačné strany. Pokud tedy porovnáme tuto hodnotu s hodnotou poloměru kruhu kolem domu, můžeme zjistit, zda letadlo bude létat dostatečně blízko, abychom ho mohli vidět. Další kousek, který můžeme udělat, je vypočítat čas, za který letadlo proletí, pomocí rychlosti vzduchu a vzdálenosti, a pokud je to méně než řekněme asi 45 sekund, rozsvítíme světlo. Toto je trochu kódu, který používám k určení šance na přelet. Dělám to, protože je nedaleké letiště, a když letadla pojíždějí, nevyhnutelně míří na dům. Protože je však jejich nadmořská výška nulová a rychlost jde pěšky, nemělo by to vyvolat poplach.

funkce get_intercept ($ home_head, $ plane_head, $ plane_distance) {

$ flight_angle = abs (abs ($ home_head - $ plane_head) - 180); $ flight_angle_r = deg2rad ($ flight_angle); $ flight_angle_t = tan ($ flight_angle_r); $ flight_intercept = $ flight_angle_t * $ plane_distance;

if (($ flight_angle <90) && ($ flight_intercept <3)) {// possible fly around

}

vrátit $ flight_intercept;

}

Krok 10: Vzdálenost mezi dvěma body na mapě - vzorec Haversine

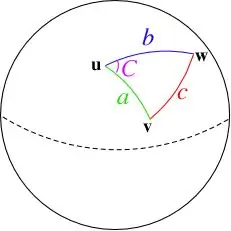
Musíme tedy vypočítat vzdálenost mezi letadlem a naší polohou. Na krátkých vzdálenostech na mapě můžete přibližně vypočítat vzdálenost, ale protože Země je sférická, existuje vzorec nazývaný vzorec haversine, který vám umožňuje vzít v úvahu zakřivený povrch. Dále si můžete přečíst vzorec:

Nyní, když je vypočítaná vzdálenost a víme o rychlosti letu letadla, můžeme vypočítat, kolik sekund bude trvat, než bude letadlo nad hlavou. Kontrolka se tedy rozsvítí, pokud je něco do 30 sekund od flypastu a konečně máme výstražné světlo.

* založené na 0n JS na instantglobe.com/CRANES/GeoCoordTool.html a změněno na PHP */

funkce get_distHaversine ($ home_lat, $ home_lon, $ plane_lat, $ plane_lon) {$ R = 6371; // střední poloměr Země v km $ dLat = deg2rad ($ plane_lat- $ home_lat); $ dLon = deg2rad ($ plane_lon- $ home_lon); $ lat1 = deg2rad ($ home_lat); $ lat2 = deg2rad ($ plane_lat);

$ a = sin ($ dLat/2) * sin ($ dLat/2) + cos ($ lat1) * cos ($ lat2) * sin ($ dLon/2) * sin ($ dLon/2);

$ c = 2 * atan2 (sqrt ($ a), sqrt (1- $ a)); $ d = $ R * $ c; vrátit $ d; }

Krok 11: Import a definování rovinné databáze

Jedním z dalších kousků je, že web opensky nabízí databázi letadel ke stažení spolu s jejich značkami a identy. Jeho několik set tisíc záznamů. Můžeme to tedy stáhnout a lokálně načíst do databáze MariaDB pro vyhledávání (MySQL). S každým letadlem, které se objeví nad hlavou, získáme jeho detaily a aktualizujeme počítadlo, abychom ukázali, kolikrát už bylo vidět.

Aktuálně také upravuji databázi, abych zvýraznil letadla, která mě zajímají. Hlavně staré válečné ptáky a další podobná zajímavá letadla. Letos v létě přeletěl Mig-15 několikrát. cílem je tedy použít výstražné pole, které jsem přidal, a poté rychle blikat světlem, když se blíží něco zajímavého

Krok 12: Vylepšení výsledků a nových funkcí

Takže teoreticky všechno funguje docela dobře, ale s údaji zjistíte, že existují letadla, která létají a která se v API neobjevují.

Důvodem je, že ne všechna letadla používají transpondér ADS-B a používají starší transpondéry založené na MLAT. Chcete -li získat údaje o poloze letadel pomocí MLAT, vyžaduje to sérii přijímačů na zemi, aby triangulovaly svou polohu, a některá místa, jako je flightradar24, mají ve srovnání s opensky větší síť přispěvatelů. Doufejme, že se časem také zlepší jejich pokrytí a nastavuji vlastní přijímač MLAT, který přidá k těmto datům.

Krok 13: Codebase

Nezapomeňte, že pokud to budete používat, možná budete chtít odstranit příkazy SQL, pokud nemáte databázi letadel, a také přidat vlastní hodnotu Lon/Lat a klíč API pro přístup k letovým datům.

github.com/ajax-jones/runway-light-awacs

define ("INTERVAL", (20 * 1)); funkce fexp () {$ lat = "vaše zeměpisná šířka"; $ lon = "vaše zeměpisná délka"; $ strana = 15,75; $ box = get_bounding_box ($ lat, $ lon, $ side); $ latmin = $ box [0]; $ lonmin = $ box [1]; $ latmax = $ box [2]; $ lonmax = $ box [3]; $ flyurl = "https://opensky-network.org/api/states/all?lamin=$latmin&lomin=$lonmin&lamax=$latmax&lomax=$lonmax"; echo „Skenování oblohy“; $ start_time = microtime (true); $ json = file_get_contents ($ flyurl); $ data = json_decode ($ json, TRUE); $ inbound = FALSE; $ num_planes = počet ($ data ['stavy']); if ($ num_planes> 0) {echo "a můžeme vidět $ num_planes letadla / n"; pro ($ x = 0; $ x 0) {$ plane_eta = $ distplane/$ air_speed_kmh; } else {$ eta = 1; } if ((($ intercept) 0)) && ($ distplane0) {$ inbound = TRUE; echo “------------------------------------------------ -------------------- / n "; echo "$ icao24 - [$ country $ callsign] na [$ geo_altitude_m M - $ geo_altitude_f ft]"; echo "[rychlost $ air_speed_kmh kmh a", kulaté ($ distplane, 1), "km daleko] n"; echo "[na záhlaví", kulaté ($ plane_heading, 1), "] [homeangle $ nadpis_d]"; echo "[$ zeměpisná šířka, $ zeměpisná délka] n"; echo "[flypast in", decimal_to_time ($ plane_eta), "now", round ($ intercept, 1), "km away / n"; echo “------------------------------------------------ -------------------- / n "; $ DBi = nový mysqli ("127.0.0.1", "root", "vaše heslo", "awacs"); $ sql = "vyberte * z databáze letadel, kde` icao24` = '$ icao24' "; mysqli_set_charset ($ DBi, "utf8"); $ getplanedata = mysqli_query ($ DBi, $ sql) nebo die (mysqli_error ($ DBi)); $ row_getplanedata = mysqli_fetch_assoc ($ getplanedata); $ row_getplanedata = mysqli_num_rows ($ getplanedata); if ($ rows_getplanedata> 0) {do {echo "callsign ="; echo $ row_getplanedata ['registrace']; echo "je"; echo $ row_getplanedata ['vyrobername']; echo ""; echo $ row_getplanedata ['model']; echo "od"; echo $ row_getplanedata ['manufacturingicao']; echo „ve vlastnictví“; echo $ row_getplanedata ['vlastník']; echo „viděno“; echo $ row_getplanedata ['návštěvy']; echo „časy“; echo "speciální hodnocení ="; echo $ row_getplanedata ['special']; echo "\ n"; $ visit = $ row_getplanedata ['návštěvy']+1; } while ($ row_getplanedata = mysqli_fetch_assoc ($ getplanedata)); mysqli_free_result ($ getplanedata); $ sqli = "AKTUALIZACE databáze letadel NASTAVTE návštěvy = $ návštěvy WHERE icao24 = '$ icao24'"; mysqli_set_charset ($ DBi, "utf8"); $ updateplanedata = mysqli_query ($ DBi, $ sqli) nebo die (mysqli_error ($ DBi)); } else {echo "Tuto rovinu nelze v DB najít, takže ji přidám"; $ sqli = "VLOŽIT DO DATABÁZE letadel (icao24, návštěvy, speciální) HODNOTY ('$ icao24', 1, 1)"; $ updateplanedata = mysqli_query ($ DBi, $ sqli) nebo die (mysqli_error ($ DBi)); } echo "----------------------------------------------- --------------------- / n "; } else {// echo "$ volací znak"; }}} else {echo "a obloha je jasná / n"; } if ($ inbound) {echo "Inbound plane / n"; $ command = "prasata w 17 1"; execInBackground (příkaz $); } else {echo "žádné příchozí lety / n"; $ command = "prasata w 17 0"; execInBackground (příkaz $); }} funkce decimal_to_time ($ decimal) {$ offset = 0,002778; if ($ decimal> $ offset) {$ decimal = $ decimal - 0,002778; } $ hours = gmdate ('H', floor ($ decimal * 3600)); $ minutes = gmdate ('i', floor ($ decimal * 3600)); $ seconds = gmdate ('s', floor ($ decimal * 3600)); vrátit str_pad ($ hodin, 2, „0“, STR_PAD_LEFT). ":". str_pad ($ minut, 2, „0“, STR_PAD_LEFT). ":". str_pad ($ sekund, 2, "0", STR_PAD_LEFT); }/ * * vypočítat (počáteční) směr mezi dvěma body * * z: Aviation Formulary Eda Williamse, https://williams.best.vwh.net/avform.htm#Crs * source = instantglobe.com/CRANES/GeoCoordTool. html */ funkce get_bearing ($ home_lat, $ home_lon, $ plane_lat, $ plane_lon) {$ lat1 = deg2rad ($ home_lat); $ lat2 = deg2rad ($ plane_lat); $ dLon = deg2rad ($ plane_lon- $ home_lon); $ y = sin ($ dLon) * cos ($ lat2); $ x = cos ($ lat1)*sin ($ lat2) - sin ($ lat1)*cos ($ lat2)*cos ($ dLon); $ z = atan2 ($ y, $ x); $ zz = (rad2deg ($ z) +360)% 360; vrátit $ zz; } funkce get_intercept ($ home_head, $ plane_head, $ plane_distance) {$ flight_angle = abs (abs ($ home_head - $ plane_head) - 180); $ flight_angle_r = deg2rad ($ flight_angle); $ flight_angle_t = tan ($ flight_angle_r); $ flight_intercept = $ flight_angle_t * $ distance_distance; vrátit $ flight_intercept; } /* - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - *// * * Pomocí Haversinova vzorce vypočítat vzdálenost (v km) mezi dvěma body určenými * zeměpisnou šířkou/délkou (v číselných stupních) * * z: Haversinův vzorec - RWSinnott, „Virtues of the Haversine“, * Sky and Telescope, sv. 68, č. 2, 1984 * https://williams.best.vwh.net/avform.htm#Crs * * příklad použití z formuláře: * result.value = LatLon.distHaversine (lat1.value.parseDeg (), long1.value.parseDeg (), * lat2.value.parseDeg (), long2.value.parseDeg ()); * kde lat1, long1, lat2, long2 a result jsou pole formuláře * source = instantglobe.com/CRANES/GeoCoordTool.html */function get_distHaversine ($ home_lat, $ home_lon, $ plane_lat, $ plane_lon) {$ R = 6371; // střední poloměr Země v km $ dLat = deg2rad ($ plane_lat- $ home_lat); $ dLon = deg2rad ($ plane_lon- $ home_lon); $ lat1 = deg2rad ($ home_lat); $ lat2 = deg2rad ($ plane_lat); $ a = sin ($ dLat/2) * sin ($ dLat/2) + cos ($ lat1) * cos ($ lat2) * sin ($ dLon/2) * sin ($ dLon/2); $ c = 2 * atan2 (sqrt ($ a), sqrt (1- $ a)); $ d = $ R * $ c; vrátit $ d; } funkce get_bounding_box ($ latitude_in_degrees, $ longitude_in_degrees, $ half_side_in_miles) {$ half_side_in_km = $ half_side_in_miles * 1,609344; $ lat = deg2rad ($ latitude_in_degrees); $ lon = deg2rad ($ longitude_in_degrees); $ radius = 6371; # Poloměr rovnoběžky v dané zeměpisné šířce; $ parallel_radius = $ radius*cos ($ lat); $ lat_min = $ lat - $ half_side_in_km/$ radius; $ lat_max = $ lat + $ half_side_in_km/$ radius; $ lon_min = $ lon - $ half_side_in_km/$ parallel_radius; $ lon_max = $ lon + $ half_side_in_km/$ parallel_radius; $ box_lat_min = rad2deg ($ lat_min); $ box_lon_min = rad2deg ($ lon_min); $ box_lat_max = rad2deg ($ lat_max); $ box_lon_max = rad2deg ($ lon_max); návratové pole ($ box_lat_min, $ box_lon_min, $ box_lat_max, $ box_lon_max); } funkce execInBackground ($ cmd) {if (substr (php_uname (), 0, 7) == "Windows") {pclose (popen ("start /B". $ cmd, "r")); } else {exec ($ cmd. "> /dev /null &"); }} funkce checkForStopFlag () {// zcela volitelný návrat (TRUE); } funkce start () {echo "začíná / n"; $ command = "prasata w 17 1"; execInBackground (příkaz $); $ aktivní = PRAVDA; while ($ active) {usleep (1000); // nepovinné, pokud chcete být ohleduplní if (microtime (true)> = $ nextTime) {fexp (); $ nextTime = mikrotime (true) + INTERVAL; } $ aktivní = checkForStopFlag (); }} fexp (); Start(); ?>

Krok 14: Zapojení LED a vypínače

Zapojení tohoto projektu nemůže být ve skutečnosti jednodušší. Existuje pouze jedna LED, která je připojena ke kolíku 17 a uzemnění vloženým odporem 270R.

Také zahrnuji tlačítko pro vypnutí a zapnutí spolu s LED diodou napájení, která běží z datového kolíku TXd. Více o funkci vypnutí a požadovaném kódu si můžete přečíst na https://github.com/Howchoo/pi-power-button.git z webu https://howchoo.com/g/mwnlytk3zmm/how-to- add-a-pow… O přidání kontrolky napájení si můžete přečíst zde