
Obsah:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:23.
- Naposledy změněno 2025-01-23 14:38.

V poslední době bylo provedeno mnoho práce na vlastním vyvažování objektů. Koncept vlastního vyvažování začal vyvažováním obráceného kyvadla. Tento koncept se rozšířil i na konstrukci letadel. V tomto projektu jsme navrhli malý model samovyvažovacího robota pomocí PID (proporcionálního, integrálního, derivačního) algoritmu. Od té doby je tato metoda novou tváří systémů řízení průmyslových procesů. Tato zpráva popisuje metody zahrnuté ve vlastním vyvažování objektů. Tento projekt byl veden jako semestrální projekt, jehož cílem bylo porozumět korelaci PID s účinností různých průmyslových procesů. Zde se soustředíme pouze na poskytnutí stručného přehledu o účinnosti a aplikaci PID řízení. Tento dokument byl vytvořen poskytnutím krátkého úvodu do řídicích systémů a souvisejících terminologií s doplněním motivací projektu. Byly provedeny experimenty a pozorování, popsány zásluhy a nedostatky s koncem budoucích vylepšení. Pro pochopení účinnosti PID ve světě řídicího systému byl vyvinut model samovyvažovacího robota. Po několika přísných testech a experimentech byly objeveny přednosti a nedostatky řídicího systému PID. Bylo zjištěno, že navzdory mnoha výhodám řízení PID oproti předchozím metodám tento systém stále vyžaduje mnoho vylepšení. Doufáme, že čtenář dobře porozumí důležitosti vlastního vyvažování, účinnosti a nedostatkům řízení PID
Krok 1: Úvod
S příchodem počítačů a industrializací procesů v celé lidské historii vždy probíhal výzkum s cílem vyvinout způsoby, jak procesy zpřesnit, a co je důležitější, ovládat je pomocí strojů autonomně. Účelem je omezit zapojení člověka do těchto procesů, a tím snížit chyby v těchto procesech. Proto byla vyvinuta oblast „Engineering Control System“. Inženýrství řídicího systému lze definovat jako používání různých metod pro řízení fungování procesu nebo udržování konstantního a preferovaného prostředí, ať už manuálního nebo automatického.
Jednoduchým příkladem může být řízení teploty v místnosti. Ruční ovládání znamená přítomnost osoby na místě, která kontroluje současné podmínky (senzor), porovnává je s požadovanou hodnotou (zpracování) a provádí příslušná opatření k získání požadované hodnoty (aktuátor). Problém této metody spočívá v tom, že není příliš spolehlivá, protože člověk je ve své práci náchylný k chybám nebo nedbalosti. Dalším problémem je také to, že rychlost procesu zahájeného aktuátorem není vždy jednotná, což znamená, že se někdy může objevit rychleji, než je požadováno, nebo někdy může být pomalý. Řešením tohoto problému bylo použití mikrořadiče k ovládání systému. Mikroprocesor je
naprogramovaný tak, aby řídil proces, podle daných specifikací, zapojený do obvodu (bude diskutováno později), přivádí požadovanou hodnotu nebo podmínky a tím řídí proces tak, aby udržoval požadovanou hodnotu. Výhodou tohoto procesu je, že do tohoto procesu není vyžadován žádný lidský zásah. Také rychlost procesu je jednotná
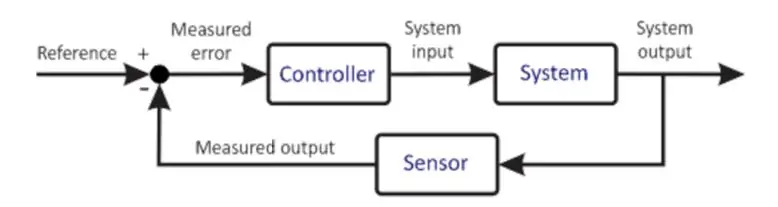
Základní řídicí systém
Předchozí diagram ukazuje velmi zjednodušenou verzi řídicího systému. Mikrokontrolér je srdcem každého řídicího systému. Je to velmi důležitá součást, proto by měl být výběr výběru proveden pečlivě na základě požadavků systému. Mikroprocesor přijímá vstup od uživatele. Tento vstup definuje požadovaný stav systému. Mikroprocesor také dostává zpětnou vazbu od senzoru. Tento senzor je připojen k výstupu systému, jehož informace jsou přiváděny zpět na vstup. Mikroprocesor na základě svého programování provádí různé výpočty a dává výstup akčnímu členu. Aktuátor na základě výkonu řídí zařízení, aby se pokusil tyto podmínky udržet. Příkladem může být řidič motoru pohánějící motor, kde ovladač motoru je akční člen a motor je závod. Motor se tedy otáčí danou rychlostí. Připojený senzor snímá aktuální stav zařízení a přivádí jej zpět do mikrořadiče. Mikroprocesor opět porovnává, provádí výpočty a cyklus se tedy opakuje. Tento proces se opakuje a je nekonečný, přičemž mikrořadič udržuje požadované podmínky
Krok 2: Řídicí systém založený na PID
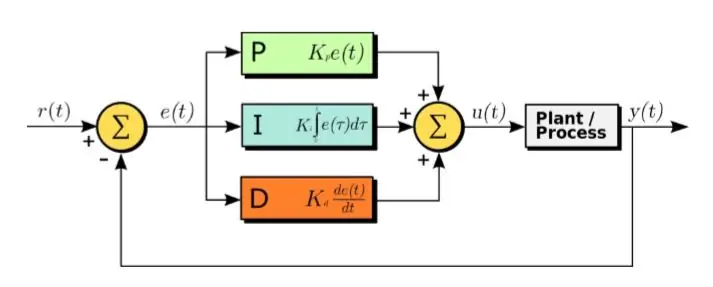

Algoritmus PID je efektivní metodou návrhu řídicího systému.
Definice
PID je zkratka pro proporcionální, integrální a derivační. V tomto algoritmu je vstupem chybový signál. A následující rovnice je aplikována na chybový signál
U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integrál (e (t)) (1,1)
Krátké vysvětlení
Jak je vidět na výše uvedené rovnici, integrál a derivace chybových signálů se vypočítají, vynásobí jejich příslušnými konstantami a sečte se s konstantou Kp vynásobenou e (t). Výstup je pak přiváděn k pohonu, který spouští systém. Nyní se podívejme postupně na každou část funkce. Tato funkce přímo ovlivňuje dobu náběhu, dobu pádu, špičku nad záběrem, dobu ustálení a chybu ustáleného stavu.
• Proporcionální část: Proporcionální část zkracuje dobu náběhu a snižuje chybu ustáleného stavu. To znamená, že systému bude trvat kratší dobu, než dosáhne své špičkové hodnoty, a když dosáhne ustáleného stavu, chyba ustáleného stavu bude nízká. Zvyšuje však překročení špiček.
• Odvozená část: Odvozená část snižuje přestřelení a dobu ustálení. To znamená, že přechodový stav systému bude více tlumen. Systém také dosáhne svého ustáleného stavu za kratší dobu. Nemá to však žádný vliv na dobu náběhu nebo chybu ustáleného stavu.
• Integrální část: Integrální část zkracuje dobu náběhu a zcela eliminuje chybu ustáleného stavu. Zvyšuje však překročení vrcholu a dobu ustálení.
• Ladění: Dobrý řídicí systém bude mít nízkou dobu náběhu, dobu ustálení, překročení špiček a chybu ustáleného stavu. Proto musí být Kp, Kd, Ki pečlivě vyladěny, aby se upravil přínos výše uvedených faktorů, aby se získal dobrý kontrolní systém.
Byl přiložen obrázek ukazující účinek změny různých parametrů v PID algoritmu.
Krok 3: Robot s vlastním vyvažováním

Samovyvažovací robot je vícevrstvý dvoukolový robot.
Robot se pokusí vyrovnat s použitím jakékoli nestejné síly. Vyrovná se sama působením síly, která je proti výslednici sil na robota.
Metody vlastního vyvažování
Existují čtyři způsoby vlastního vyvažování robotů. Jedná se o následující:
Samovyvažování pomocí dvou infračervených snímačů náklonu
Toto je jeden z nejhrubších způsobů vyvážení robota, protože vyžaduje velmi málo hardwaru a relativně snadný algoritmus. V tomto přístupu se k měření vzdálenosti mezi zemí a robotem používají dva nakloněné IR senzory. Na základě vypočtené vzdálenosti lze PID použít k pohonu motorů k odpovídajícímu vyvážení robota. Jednou nevýhodou této metody je, že IR senzor může vynechat některá měření. Dalším problémem je, že pro výpočet vzdálenosti je nutné přerušení a smyčky, což zvyšuje časovou složitost algoritmu. Tato metoda vyvažovacího robota proto není příliš účinná.
Samovyvažování pomocí akcelerometru
Akcelerometr nám udává zrychlení těla ve 3 osách. Zrychlení orientované v ose y (nahoru) a v ose x (vpřed) nám dává míru pro výpočet směru gravitace, a tedy pro výpočet úhlu sklonu. Úhel se vypočítá následovně:
θ = arktan (Ay/Ax) (1,2)
Nevýhodou použití této metody je, že během pohybu robota bude k odečtům přidáno také horizontální zrychlení, což je vysokofrekvenční šum. Proto bude úhel sklonu nepřesný.
Samovyvažování pomocí gyroskopu
Pro výpočet úhlových rychlostí podél tří os se používá gyroskop. Úhel sklonu se získá pomocí následující rovnice.
θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1,3)
Jednou velkou nevýhodou použití gyroskopu je, že má malý DC Bias, což je nízkofrekvenční šum, a za několik časů jsou vrácené hodnoty zcela špatné. To po integraci způsobí posunutí nulového bodu. V důsledku toho robot nějakou dobu zůstane ve svislé poloze a převrhne se, jakmile přijde drift.
Samovyvažování pomocí akcelerometru i gyroskopu
Jak bylo uvedeno výše, použití pouze akcelerometru nebo gyroskopu nám neposkytne správný úhel sklonu. K tomu se používá akcelerometr i gyroskop. Oba jsou vloženy do MPU6050. V tomto případě získáme data z obou z nich a poté je spojíme buď pomocí Kalmanova filtru, nebo doplňkového filtru.
• Kalmanův filtr: Kalmanův filtr vypočítává nejlepší odhad stavu dynamického systému z hlučných měření a minimalizuje průměrnou čtvercovou chybu odhadu. Funguje ve dvou fázích, predikci a korekci, vzhledem k diskrétním stochastickým rovnicím popisujícím dynamiku systému. Je to však velmi složitý algoritmus, který lze implementovat zejména na omezeném hardwaru mikrokontroléru.
• Doplňkový filtr: Tento algoritmus primárně využívá data získaná z gyroskopu a v průběhu času je integruje, aby získal úhel sklonu. Využívá také malý podíl naměřených hodnot akcelerometru. Doplňkový filtr ve skutečnosti minimalizuje vysokofrekvenční hluk akcelerometru a nízkofrekvenční šum gyroskopu a poté je spojí, aby poskytl nejlepší přesný úhel sklonu.
Krok 4: Návrh robota
Navrhli jsme samovyvažovacího robota pomocí proporcionálního derivačního ovladače implementovaného komplementárním filtrem pro MPU6050. Tento malý model robota s vlastním vyvažováním nám ukáže užitečnost řídicích systémů při samovyvažování robotů.
Implementace systému:
Systém je samovyvažovací robot. Implementuje se pomocí PID řadiče, což je proporcionální integrovaný derivační řadič. Robota vyvažujeme tak, že pojíždíme jeho kola ve směru jeho pádu. Při tom se snažíme udržet těžiště robota nad otočným bodem. Abychom poháněli kola ve směru jeho pádu, měli bychom vědět, kam robot padá a jakou rychlostí padá. Tato data jsou získána pomocí MPU6050, který má akcelerometr a gyroskop. MPU6050 měří úhel sklonu a dává výstup mikrořadiči. MPU6050 je propojen s deskou STM prostřednictvím I2C. V I2C je jeden vodič pro hodiny, které jsou pojmenovány jako SCL. Druhý je pro přenos dat, který je SDA. V tomto se používá komunikace master slave. Počáteční adresa a koncová adresa je specifikována tak, aby věděla, odkud data začínají a kde končí. Zde jsme implementovali doplňkový filtr pro MPU6050, což je matematický filtr pro sloučení výstupů akcelerometru a gyroskopu. Po získání dat z MPU6050 provede mikrokontrolér výpočty, aby věděl, kam padá. Na základě výpočtů bude mikrořadič STM dávat řidiči motoru povely k řízení vozidel ve směru pádu, což vyváží robota.
Krok 5: Součásti projektu



V projektu samovyvažovacího robota byly použity následující komponenty:
STM32F407
Mikroprocesor navržený společností ST Microelectronics. Funguje na architektuře ARM Cortex-M.
Ovladač motoru L298N
Tento IC slouží k chodu motoru. Získá dva externí vstupy. Jeden z mikrokontroléru, který mu dodává signál PWM. Nastavením šířky impulzu lze nastavit otáčky motoru. Jeho druhým vstupem je zdroj napětí potřebný k pohonu motoru, což je v našem případě baterie 12V.
DC motor
Stejnosměrný motor běží na stejnosměrné napájení. V tomto experimentu běží stejnosměrný motor pomocí optočlenů připojených k ovladači motoru. K pohonu motoru jsme použili Motor Drive L298N.
MPU6050
MPU6050 se používá k získání informací o tom, kam robot padá. Měří úhel sklonu vzhledem k bodu nulového sklonu, což je poloha MPU6050 při spuštění programu.
MPU6050 má 3osý akcelerometr a 3osý gyroskop. Akcelerometr měří zrychlení podél tří os a gyroskop měří úhlovou rychlost kolem tří os. Abychom spojili výstup, musíme odfiltrovat zvuky obou. Abychom filtrovali zvuky, máme Kalmanův a doplňkový filtr. Do našeho projektu jsme implementovali doplňkový filtr.
Opto pár 4N35
Optočlen je zařízení používané k izolaci nízkonapěťové a vysokonapěťové části obvodu. Jak název napovídá, funguje na bázi světla. Když část nízkého napětí dostane signál, proud proudí v části vysokého napětí
Krok 6: Struktura robota
Struktura robota je vysvětlena následovně:
Fyzická struktura
Samovyvažovací robot se skládá ze dvou vrstev vyrobených z průhledného plastového skla. Podrobnosti o dvou vrstvách jsou uvedeny níže:
První vrstva
Ve spodní části první vrstvy jsme umístili článek pro napájení desky STM. Také dva motory 4 volty byly umístěny na každé straně s pneumatikami připojenými k pohybu robota. V horní části první vrstvy byly pro provoz motorů umístěny dvě baterie po 4 voltech (celkem 8 voltů) a IC ovladače motoru (L298N).
Druhá vrstva
V horní vrstvě robota jsme umístili desku STM na Perf Board. Na vrchní vrstvu je umístěna další deska se 4 optočleny. Gyroskop je také umístěn na horní vrstvu robota ze spodní strany. Obě složky jsou umístěny ve střední části tak, aby bylo těžiště udržováno co nejníže.
Těžiště robota
Těžiště je udržováno co nejníže. Za tímto účelem jsme na spodní vrstvu umístili těžké baterie a na horní vrstvu lehké komponenty, jako jsou desky STM a optočleny.
Krok 7: Kód
Kód byl sestaven na Atollic TrueStudio. K ladění bylo použito STM studio.
Krok 8: Závěr
Po spoustě experimentování a pozorování se nakonec dostáváme k bodu, kde shrnujeme naše výsledky a diskutujeme o tom, jak daleko se nám podařilo implementovat a vypracovat efektivitu systému.
Obecná kontrola
Během experimentování byla rychlost motoru úspěšně řízena pomocí algoritmu PID. Křivka však není přesně hladká přímka. Existuje pro to mnoho důvodů:
• Senzor, i když je připojen k nízkoprůchodovému filtru, stále poskytuje určité konečné odskakování; tyto jsou způsobeny nelineárními odpory a některými nevyhnutelnými důvody analogové elektroniky.
• Motor se při malém napětí nebo PWM neotáčí plynule. Poskytuje trhnutí, které by mohlo způsobit nesprávné hodnoty přiváděné do systému.
• Kvůli kolísání může senzor postrádat některé štěrbiny poskytující vyšší hodnoty. • Dalším hlavním důvodem chyb může být základní taktovací frekvence mikrokontroléru STM. Tento model mikrokontroléru STM poskytuje takt jádra 168 MHz. Ačkoli se tento problém v tomto projektu zabýval, existuje obecná představa o tomto modelu, že neposkytuje přesně tak vysokou frekvenci.
Rychlost otevřené smyčky poskytuje velmi hladkou linku pouze s několika neočekávanými hodnotami. Algoritmus PID funguje také velmi dobře a poskytuje velmi nízkou dobu usazení motoru. Algoritmus PID motoru byl testován při různých napětích při zachování konstantních referenčních otáček. Změna napětí nezmění otáčky motoru, což ukazuje, že algoritmus PID funguje správně
Účinnost
Zde diskutujeme o účinnosti PID regulátoru, který jsme pozorovali během experimentování.
Jednoduchá implementace
V sekci experimentování a pozorování jsme viděli, že PID regulátor je velmi snadno implementovatelný. Vyžaduje pouze tři parametry nebo konstanty, které je třeba nastavit, aby měl systém řízení rychlosti
Bezkonkurenční účinnost pro lineární systémy
Lineární PID regulátor je nejefektivnější v řadě regulátorů, protože logika je velmi jednoduchá a aplikace je rozšířená v případě lineárních nebo poměrně lineárních aplikací.
Omezení
Abstraktně jsme vysvětlili omezení tohoto systému. Zde diskutujeme o několika z nich, které jsme pozorovali.
Výběr konstant
Viděli jsme, že i když je PID regulátor snadno implementovatelný, stále je hlavní nevýhodou systému, že krok výběru hodnoty konstant je pracný; protože je třeba provádět obtížné výpočty. Druhým způsobem je metoda hitu a pokusu, ale to také není účinné.
Konstanty nejsou vždy konstantní
Experimentální výsledky ukázaly, že pro různé hodnoty referenčních otáček motoru selhal PID regulátor pro stejné hodnoty konstant PID. Pro různé rychlosti musely být konstanty zvoleny odlišně a to exponenciálně zvyšuje výpočetní náklady.
Nelineární
V našem případě použitý PID regulátor je lineární, proto jej lze použít pouze na lineární systémy. U nelineárních systémů musí být regulátor implementován odlišně. Přestože jsou k dispozici různé nelineární metody PID, vyžadují výběr více parametrů. To opět činí systém nežádoucím z důvodu vysokých výpočetních nákladů.
Počáteční stisk nutný
V sekci experimentů jsme ukázali, že pro poměrně malou referenční rychlost, kde je chyba na začátku poměrně malá, je PWM dodávaný PID tak malý, že nevytváří požadovaný rozběhový moment pro motor. Motor tedy v některých pokusech neběží nebo v jiných pokusech poskytuje velké překročení a delší dobu usazování.
Krok 9: Zvláštní poděkování
Zvláštní poděkování patří členům mé skupiny, kteří mi s tímto projektem pomohli.
Odkaz na video brzy nahraji.
Doufám, že vás tento návod bude zajímat.
Toto je Tahir Ul Haq z odhlášení UET. Na zdraví !!!
Doporučuje:
Robot s vlastním vyvažováním - Algoritmus řízení PID: 3 kroky

Self Balancing Robot - PID Control Algorithm: Tento projekt byl koncipován, protože jsem měl zájem dozvědět se více o Control Algorithms a jak efektivně implementovat funkční PID smyčky. Projekt je stále ve fázi vývoje, protože ještě bude přidán modul Bluetooth, který bude
Samovyvažovací robot od Magicbit: 6 kroků

Robot s vlastním vyvažováním od Magicbit: Tento tutoriál ukazuje, jak vytvořit robota s vlastním vyvážením pomocí vývojové desky Magicbit. Jako vývojovou desku v tomto projektu, který je založen na ESP32, používáme magicbit. V tomto projektu lze tedy použít jakoukoli vývojovou desku ESP32
Dvoukolový samovyvažovací robot: 7 kroků

Dvoukolový samovyvažovací robot: Tento návod projde procesem návrhu a sestavení samovyvažovacího robota. Jako poznámku chci jen říci, že roboti s vlastním vyvažováním nejsou novým konceptem a byli postaveni a zdokumentováni ostatními. Chci využít této příležitosti
Kordický algoritmus využívající VHDL: 4 kroky
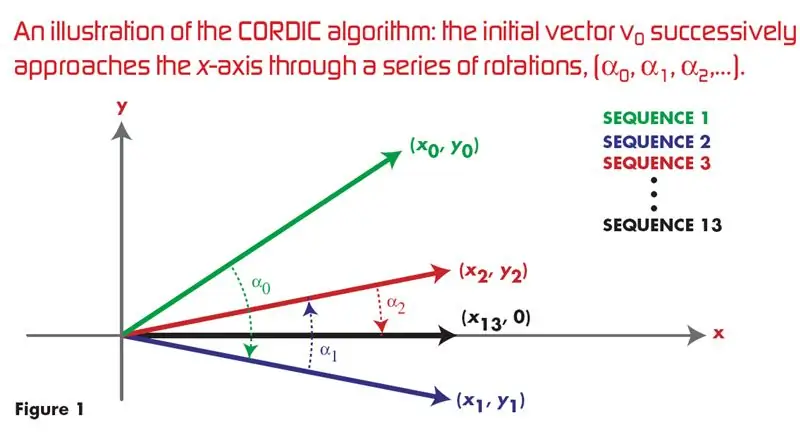
Kordický algoritmus využívající VHDL: ## Toto je nejklikanější a nejpopulárnější odkaz na Googlu pro implementaci VHDL CORDIC ALGORITHM pro generování sinusové a kosinusové vlny ## V současné době existuje mnoho hardwarově efektivních algoritmů, které však nejsou dobře známy. dominance softwaru
Jak vytvořit dálkově ovládaný 3D tištěný samovyvažovací robot: 9 kroků (s obrázky)

Jak vytvořit dálkově ovládaný 3D tištěný samovyvažovací robot: Toto je evoluce předchozí verze B-robota. 100% OTEVŘENÝ ZDROJ / robot Arduino. KÓD, 3D díly a elektronika jsou otevřené, takže je můžete upravit nebo vytvořit obrovskou verzi robota. Pokud máte pochybnosti, nápady nebo potřebujete pomoc, udělejte
