Víte o nastavení ADP ESP32 ?: 29 kroků

2024 Autor: John Day | [email protected]. Naposledy změněno: 2024-01-30 08:22

Dnes budu mluvit o techničtějším problému, ale myslím, že každý, kdo pracuje s ESP32, by měl vědět: problém úpravy čtení ADC (převodník analogového signálu na digitální). Považuji to za důležité, protože při „měření“, zejména u přístroje s analogovým výstupem, si musíte být naprosto jisti, že čtení probíhá správně.

V dnešním videu proto provedeme měření pomocí „analogově-digitálního převaděče“ESP32, sledujeme rozdíly v převodu a použijeme metodu úpravy / kalibrace ADC.

Krok 1: Co je to AD Converter?

Převodník AD je obvod schopný převádět analogovou (spojitou) veličinu na digitální (diskrétní) hodnoty. Co to znamená? To znamená, že zatímco digitální hodnoty mohou nabývat pouze diskrétních hodnot tvořených kombinací nul a jedniček, analogová veličina může nabývat jakékoli hodnoty v rozsahu. Pokud bychom například změřili napětí ideálního článku AA, mohli bychom najít libovolnou hodnotu mezi 0 V a 1,5 V, protože se jedná o analogovou veličinu. Výstupní stav ideální lampy musí předpokládat pouze dva stavy (vypnuto nebo zapnuto), což je diskrétní velikost. Protože mikrokontroléry pracují s touto diskrétní logikou, potřebujeme obvod schopný převést analogovou veličinu na digitální (nebo diskrétní).

Krok 2: Použité zdroje

• Jedna karta Lolin32 Lite v1.0.0

• Osciloskop Tektronix TDS1001C pro snímání

• Jeden USB kabel pro ESP32

• Osciloskop Hantek DSO4102C jako generátor signálu

Krok 3: ESP32 ADC

Podle údajů společnosti Espressif mohou čipy ESP32 v měřených výsledcích představovat +/- 6% rozdíl od jednoho čipu k druhému.

Kromě toho převod NEMÁ lineární odpověď na každý dostupný rozsah pro čtení. Espressif poskytuje metodu kalibrace a navrhuje, aby uživatelé implementovali jiné metody, pokud to považují za nutné k dosažení požadované přesnosti.

Provedeme sběr dat, a z toho ukážeme reakce ADC a příklad použití matematického postupu pro čtení úpravy.

Existuje několik (jednodušších nebo složitějších) způsobů, jak tyto opravy provést. Je na vás, abyste vyhodnotili nejvhodnější pro váš projekt.

Ten zde zobrazený bude mít ilustrativní účel a pokusí se řešit zajímavé body, které lze pozorovat během úprav.

Krok 4: Použitý obvod

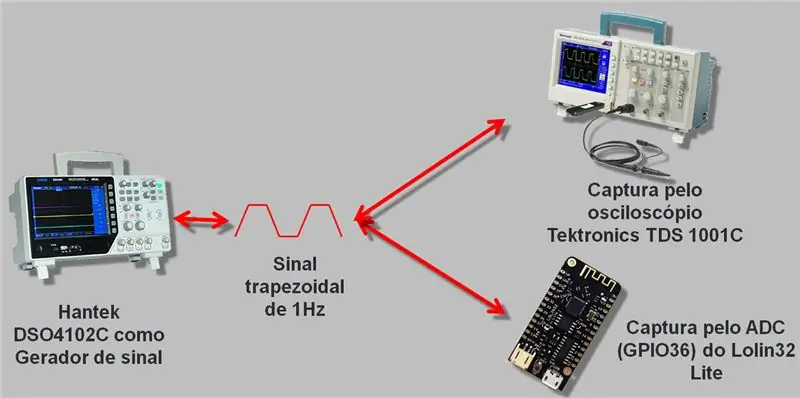
Použil jsem osciloskop s generátorem signálu, který jde až do 25 MHz, Hantek DSO4102C. Vygenerovali jsme vlnu, která byla čtena ESP A / D a osciloskopem. Shromážděná data byla zaznamenána do csv a do tabulky, kterou nechám na konci článku ke stažení.

Krok 5: Znamení použité

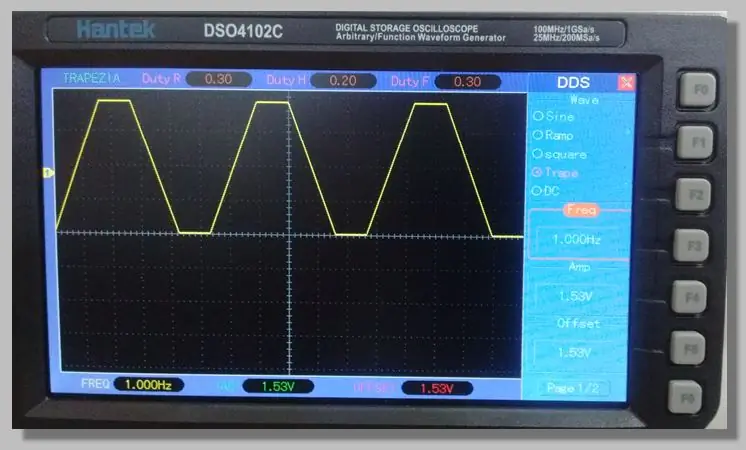
Vybrali jsme nízkofrekvenční lichoběžníkový signál, který umožňuje přístup k rampám, které procházejí celým převodním rozsahem. To umožňuje velký počet vzorků na těchto rampách.

Krok 6: Data získaná osciloskopem

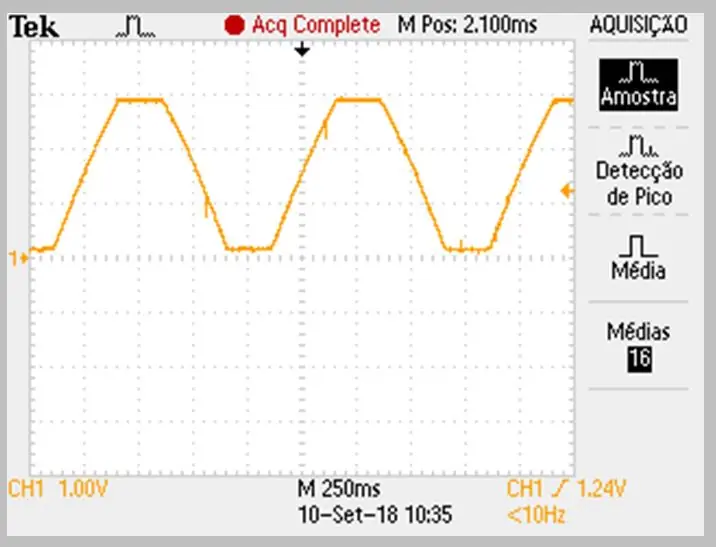
Obraz zachycení byl proveden osciloskopem. Data byla uložena v souboru CSV. Všimněte si mírného zakřivení stoupajících a klesajících ramp signálu.

Krok 7: Data získaná osciloskopem (soubor CSV v aplikaci Excel)

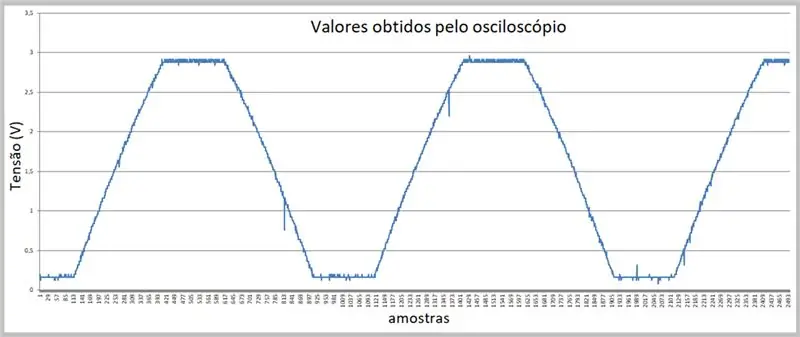
Máme zde vzorky.

Krok 8: Data získaná ADC

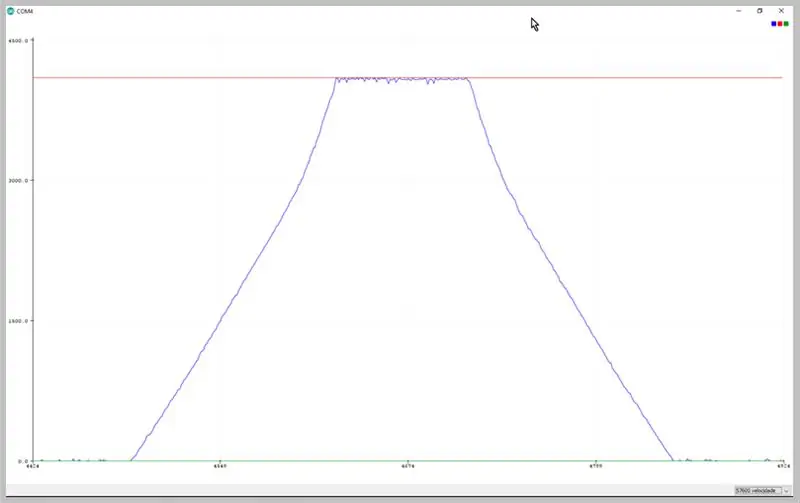
Změnou přenosové rychlosti seriálu můžeme zobrazit data zachycená ADC. Sledujte deformaci lichoběžníkového signálu.

Data pozorována na sériovém plotru Arduino IDE

Krok 9: Data získaná pomocí ADC - Excel

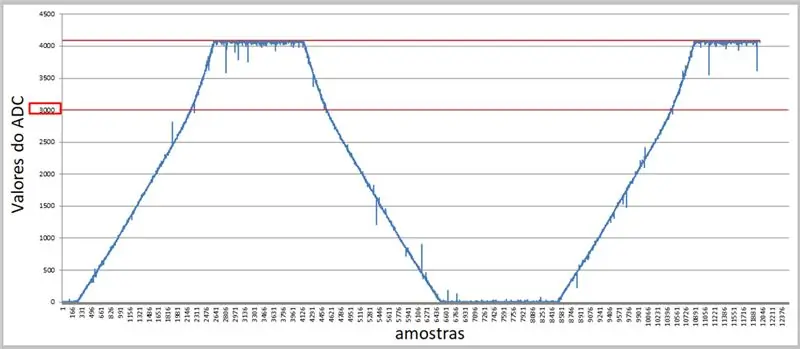
Pomocí vyšší rychlosti a sériového terminálu můžeme hodnoty zachytit a použít je v aplikaci Excel pro naše srovnání.

Krok 10: Porovnání stoupacích ramp

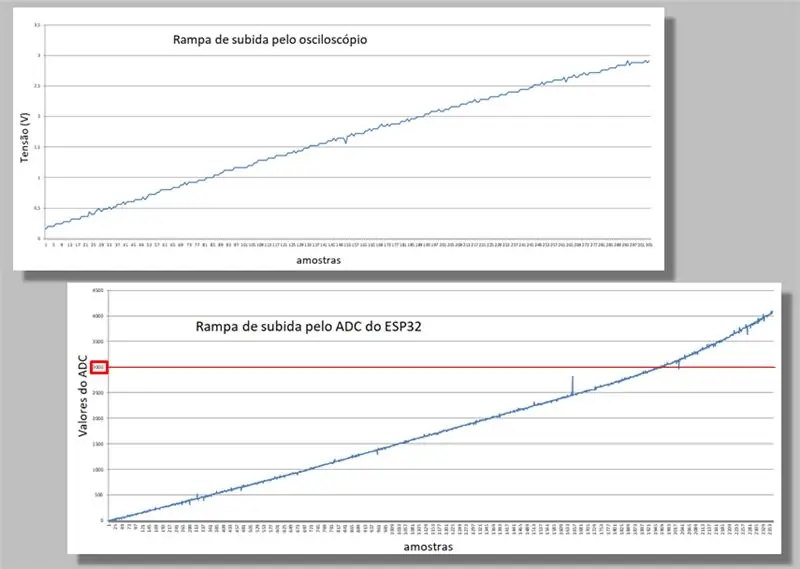
Porovnáváme dvě lezecké rampy obou úlovků.

Všimněte si zakřivení, které se vyskytuje na obou rampách.

Všimněte si také, že pro stejnou rampu máme mnohem více vzorků ESP32 než z osciloskopu.

Krok 11: Vyrovnání počtu vzorků

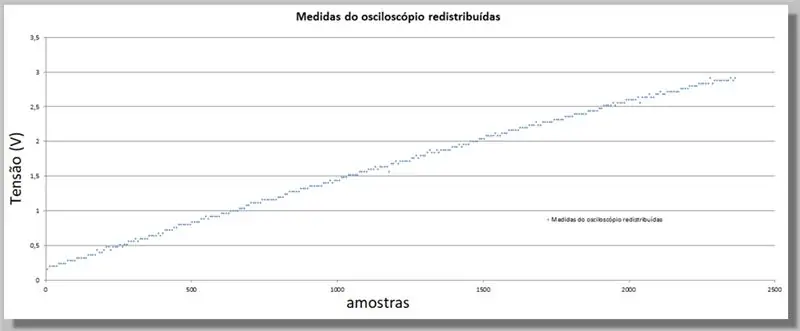
Protože ESP32 poskytoval větší počet vzorků než osciloskop, musíme tyto hodnoty srovnat, protože budou sloužit jako index pro porovnání obou křivek.

Za tímto účelem provedeme přímé srovnání.

Máme 305 vzorků pro rampu osciloskopu a 2365 vzorků pro rampu ADC.

Protože rampy jsou stejného rozsahu, můžeme říci, že pro každý osciloskop máme přibližně 7,75 vzorků ADC.

Násobení indexu každého vzorku osciloskopu má stejnou křivku, ale s indexy ekvivalentními ADC a přerozdělenými daty.

Abychom doplnili chybějící data pro nové pozice, použijeme křivku, která statisticky odpovídá známým datům.

Krok 12: Vyplnění mezer - Trend Line

Výběrem známých dat (modré tečky) kliknutím a kliknutím pravým tlačítkem vybereme: „Přidat řádek trendu…“

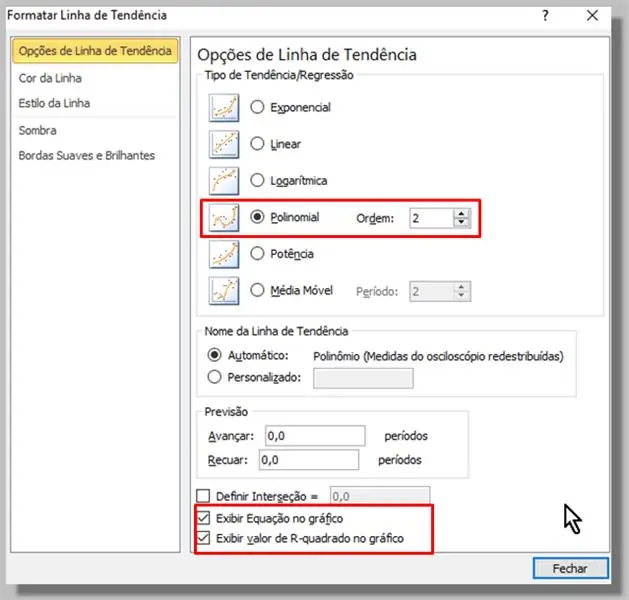
V zobrazeném okně vybereme typ Polynom (bude stačit pořadí 2).

Zkontrolovali jsme také možnosti „Zobrazit rovnici v grafu“a „Zobrazit hodnotu R na druhou v grafu“.

Klikneme na „Zavřít“.

Krok 13: Vyplnění mezer - polynomická křivka stupně 2

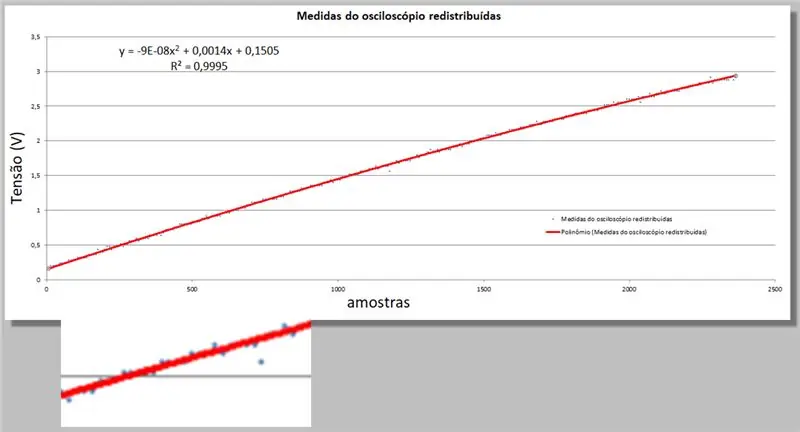
Excel nám poskytuje dvě nové informace; rovnice druhého řádu, která nejlépe odpovídá datům, a rovnice R na druhou, která kvantifikuje tuto přiměřenost.

Pamatujte, že čím blíže k 1, tím je rovnice vhodnější.

Nezabývejme se zahrnutou matematikou, použijme ji pouze jako nástroj.

Krok 14: Vyplnění mezer - vyhodnocení funkce

Vyplňme mezery ve vzorkování daty generovanými rovnicí. A pak je porovnejte bod po bodu.

y = -9E -08x2 + 0, 0014x + 0, 1505

R2 = 0, 9999

Napětí osciloskopu = -9E -08 * index2 + 0, 0014 * index + 0, 1505

Krok 15: Převod napětí osciloskopu na ekvivalentní hodnotu pro srovnání s ADC

Pojďme toho využít k transformaci hodnoty napětí osciloskopu na ekvivalentní hodnotu ADC.

Protože nejvyšší hodnota získaná v ADP ESP32 byla 4095, což odpovídá odečtu 2,958 V pro stejný index, můžeme říci, že:

Každý volt v měřeních osciloskopu se rovná přibližně 1384,4 jednotkám AD. Všechna měření osciloskopu tedy můžeme vynásobit touto hodnotou.

Krok 16: Porovnání dvou získaných ramp

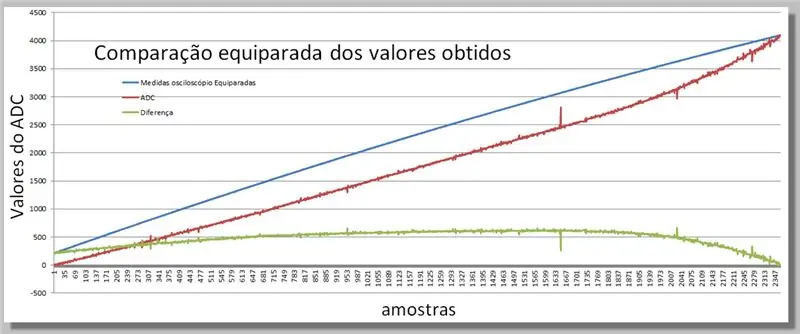
Vizualizace rozdílů získaných ve dvou odečtech.

Krok 17: Chování rozdílu čtení ADC (ERROR)

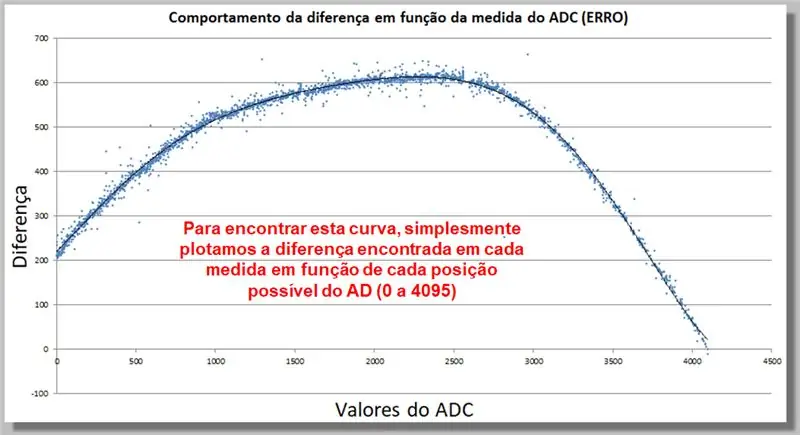
Křivka níže ukazuje, jak se rozdíl ve čtení ADC chová jako funkce měření. Tato sbírka dat nám umožní najít opravnou funkci.

Abychom našli tuto křivku, jednoduše vykreslíme rozdíl nalezený v každém taktu jako funkci každé možné polohy AD (0 až 4095).

Krok 18: Rozdílné chování čtení ADC - nalezení funkce opravy

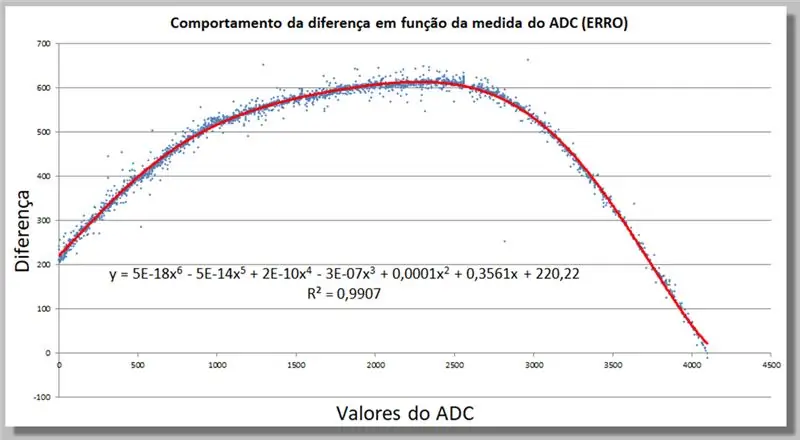
V aplikaci Excel můžeme určit opravnou funkci přidáním trendové čáry, nyní vyššího stupně, dokud nebude dostatečně odpovídat našim datům.

Krok 19: Použití jiného softwaru

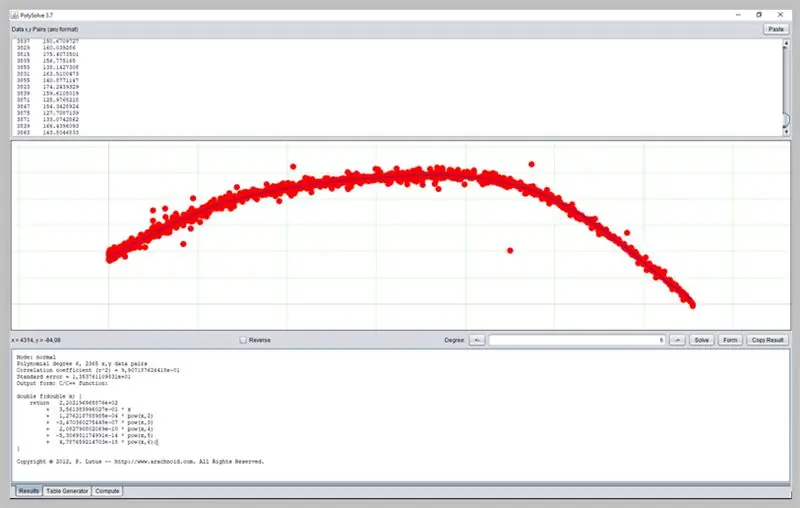
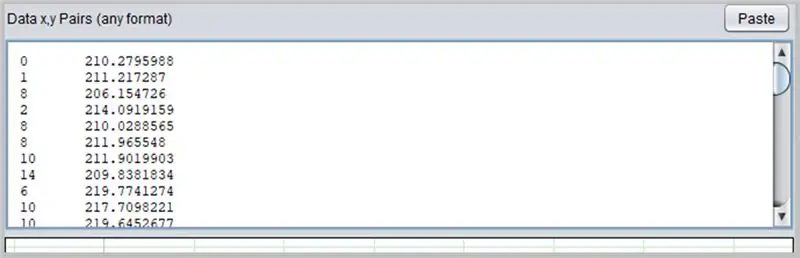
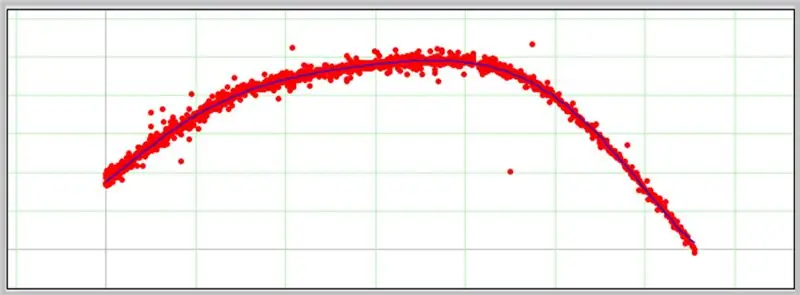
Dalším zajímavým softwarem pro určování křivek je PolySolve, který lze použít přímo na odkazu: https://arachnoid.com/polysolve/ nebo stáhnout jako Java aplikaci.

Umožňuje aplikaci polynomiálních regresí vyššího stupně a dodání formátované funkce a dalších funkcí.

Chcete -li jej použít, jednoduše zadejte data do prvního textového pole. Data musí odpovídat pořadí X, Y oddělená čárkou nebo tabulátorem. Při správném používání tečky jako desetinné čárky buďte opatrní.

Pokud jsou zadaná data správně formátována, v dalším poli se zobrazí graf.

Takto probíhala naše křivka chyb ADC.

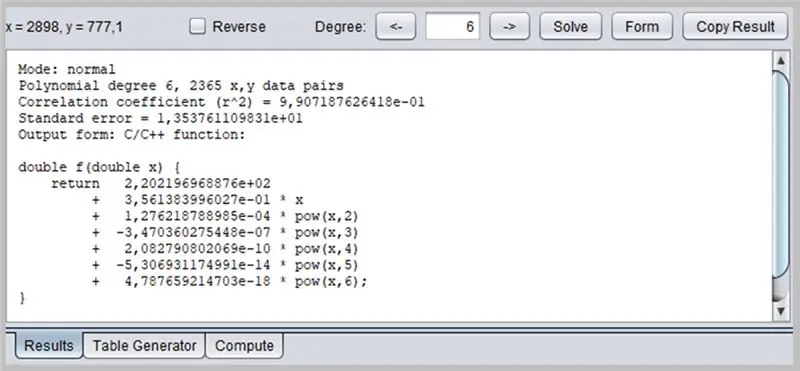
Toto okno představí výsledek regrese, včetně údajů o adekvátnosti funkcí, které zase mohou mít výstup formátovaný několika způsoby: jako funkce C / C ++, seznam koeficientů, funkce napsaná v Javě atd.

Poznámka: Věnujte pozornost oddělovačům desetinných míst

Krok 20: Konstanty a nastavení ()

Zde poukazuji na GPIO používané pro analogové snímání. Inicializuji sériový port i pin určený pro analogové snímání.

const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciando a porta serial someente para debug pinMode (pin_leitura, INPUT); // Pino využití pro analogové zachycení}

Krok 21: Smyčka () a funkce opravy

Provedeme zachycení upraveného napětí a hodnoty vytiskneme se správnými opravami nebo bez nich.

void loop () {int valor_analogico = analogRead (pin_leitura); // realiza a captura da tensão ajustada //Serial.print(valor_analogico + f (valor_analogico)); // načítání hodnot valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // impimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Serial.println (0); // cria uma linha para marcar o valor mínimo de 0}

Všimněte si v řádku 12, že máme možnost tisknout data s přidáním rozdílové funkce f (analog_value).

Krok 22: Použití funkce PolySolve Correction

Zde používáme funkci PolySolve uvnitř Arduino IDE.

/* Režim: normální Polynomiální stupeň 6, 2365 x, y datové páry Korelační koeficient (r^2) = 9, 907187626418e-01 Standardní chyba = 1, 353761109831e+01 Výstupní forma: Funkce C/C ++: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Všechna práva vyhrazena. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3,470360275448e-07 * pow (x, 3) + 2,082790802069e- 10 * prášek (x, 4) + -5,306931174991e-14 * prášek (x, 5) + 4,787659214703e-18 * prášek (x, 6); }

Všimněte si změny čárkou po tečce jako oddělovače desetinných míst.

Krok 23: Zachycení s korekcí - sériový plotter

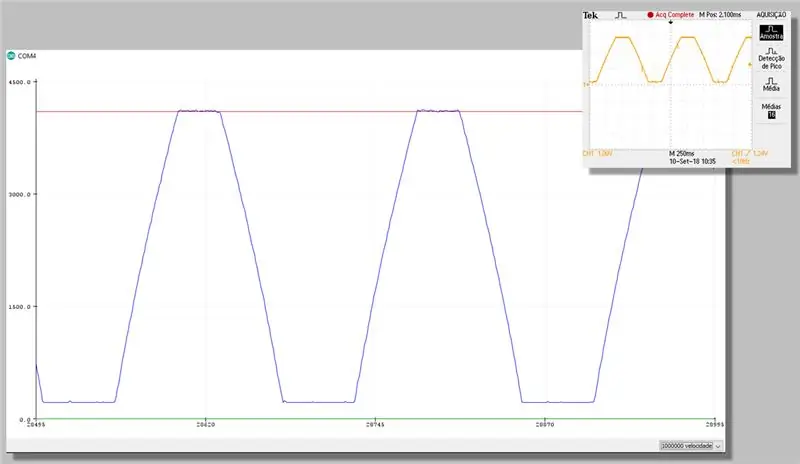
Krok 24: Výpočetní náklady

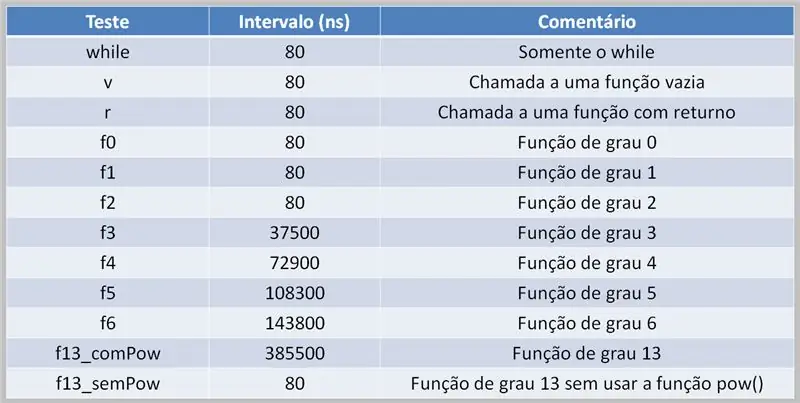
K provádění polynomiálních výpočtů je nutné, aby procesor tuto úlohu zvládl. To může vést ke zpoždění při provádění v závislosti na zdrojovém kódu a dostupném výpočetním výkonu.

Zde vidíme výsledkovou tabulku testu využívající vícestupňové polynomy. Všimněte si rozdílu mezi časy, kdy byla použita funkce pow () a kdy nebyla.

Krok 25: Testovací kód - nastavení () a spuštění smyčky ()

Zde máme kód použitý v našem testu.

neplatné nastavení () {Serial.begin (10 000 000); // Iniciando a porta serial someent para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000,0; // quantidade de chamadas float contador = 0,0; // contador de chamadas

Krok 26: Testovací kód - smyčka () a zpracování

K získání hodnoty v mikrosekundách jsem použil funkci micros ().

// ============== inicia o processo float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a fun POW contador ++; } agora = (micros () - agora) / quantidade; // určování intervalo que se passou para cada iteração // ============== finaliza o processo

Krok 27: Testovací kód - Smyčka () - Výsledky

Vytiskneme hodnotu vrácenou z funkce stupně 13 s POW a bez pro srovnání, stejně jako interval zpracování.

// časová náročnost zpětného odběru ze 13 barev POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a funkce POW Serial.print (" -"); // čas do procesu Serial.println (agora, 6); }

Krok 28: Testovací kód - použité funkce

Prázdné funkce (pouze s návratem) stupně 0 a 1.

// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2,202196968876e + 02 + 3,561383996027e-01 * x; }

Funkce stupně 2, 3 a 4.

// FUNÇÃO DE GRAU 2double f2 (double x) {return 2,202196968876e + 02 + 3,561383996027e-01 * x + 1,276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3,470360275448e-07 * pow (x, 3); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3,470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * prášek (x, 4); }

Funkce stupně 5 a 6.

// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3,470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * prášek (x, 4) + -5,306931174991e-14 * prášek (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3,470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * prášek (x, 4) + -5,306931174991e-14 * prášek (x, 5) + 4,787659214703e-18 * prášek (x, 6); }

Funkce 13. stupně pomocí POW.

// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * prášek (x, 7) + 1, 910015248179e-21 * prášek (x, 8) + -3, 566607830903e-25 * prášek (x, 9) + 5, 000280815521e-30 * prášek (x, 10) + 3, 434515045670e-32 * prášek (x, 11) + -1, 407635444704e-35 * prášek (x, 12) + 9, 871816383223e-40 * prášek (x, 13); }

Funkce třídy 13 bez použití POW.

// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + x 1, 220894795714e-14 * x * x * x * x * x * * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x * x + + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x * x; }

Krok 29: Soubory

Stáhnout soubory:

PDF

INO

Tabulkový procesor