Rekurzivní shrnutí pole v Javě: 9 kroků

2025 Autor: John Day | [email protected]. Naposledy změněno: 2025-01-23 14:38

Rekurze je velmi užitečný a časově efektivní postup, který může rychle vyřešit problém s velmi malým kódem. Rekurze zahrnuje vámi vytvořenou metodu, která zkracuje původní problém.

V tomto případě budeme sčítat pole 10 celých čísel, ale velikost může být libovolná.

Zásoby

Měli byste znát základní syntaxi javy a mít IDE nebo textový editor pro napsání kódu pro tento úkol.

Krok 1: Nastavte hlavní metodu

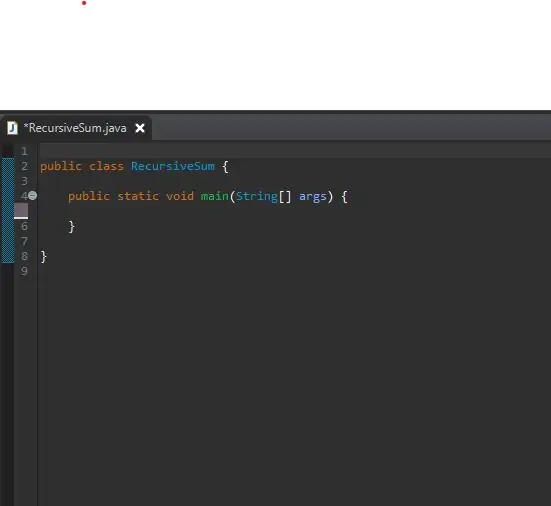
Chcete -li začít, nastavte svou hlavní metodu v nově vytvořené třídě. Svou třídu jsem pojmenoval RecursiveSum. Zde vytvoříte řadu celých čísel a zavoláte rekurzivní metodu.

Krok 2: Vytvořte záhlaví rekurzivní metody

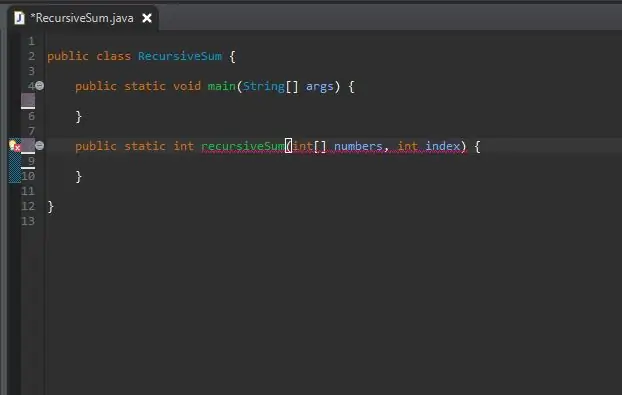
Mimo hlavní metodu vytvořte záhlaví metody pro rekurzivní metodu.

Metoda je statická, protože nebude vyžadovat, aby na ní objekt používal.

Návratový typ je int, protože pole, které budeme používat, bude plné na celá čísla. To však lze změnit na jakýkoli typ čísla, který pole obsahuje.

Svou metodu jsem pojmenoval recursiveSum, která bude mít dva parametry; pole celých čísel a index, který přidáme k součtu. Zavolal jsem těmto parametrům čísla a index.

Právě teď uvidíte chyby a to je v pořádku. Budou opraveny později.

Krok 3: Vytvořte si pouzdro Kicker/Base

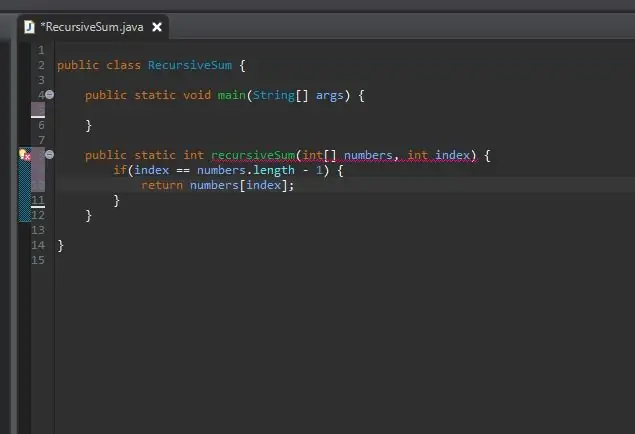
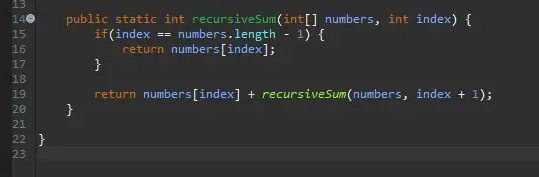
Rekurzivní metoda vyžaduje kicker/base case. To je podmínka, která zabrání vaší metodě v nekonečném volání sama. Tento základní případ lze považovat za nejjednodušší případ, se kterým se setkáme. V tomto případě bude základní případ, když jsme na konci našeho pole. Pokud se aktuální index rovná délce pole (minus 1, protože pole začínají počítat od 0, nikoli 1), jsme na konci a tento prvek v tomto indexu jednoduše vrátíme.

Krok 4: Rekurzivní krok

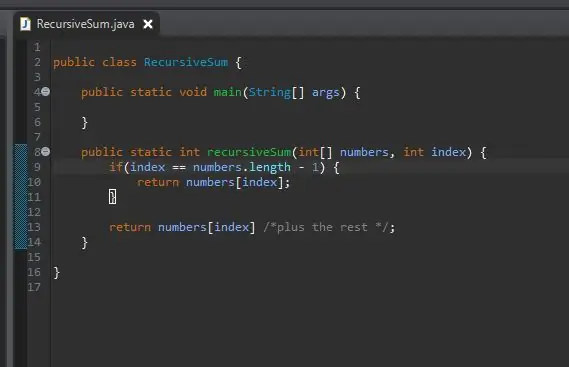
Jakmile máme základní případ, dalším krokem je náš rekurzivní krok. Tady se děje kouzlo. Řešili jsme případ, kdy se náš index rovná poslednímu prvku v našem poli. Co když nejsme u posledního prvku v našem poli? Co kdybychom tomu jednoduše řekli, aby přidal náš aktuální prvek plus další? Nakonec dosáhneme konce našeho pole a náš základní případ bude mít vliv.

Abychom toho dosáhli, jednoduše vrátíme aktuální index a „přidáme zbytek“pole.

Krok 5: Zkraťte problém

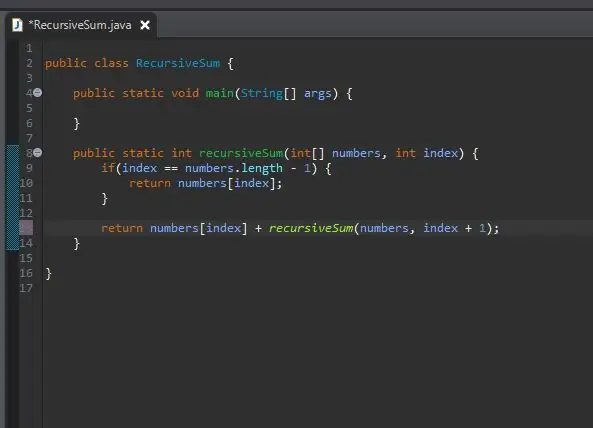
Jak jednoduše „přidáme zbytek“? Již máme metodu, která přidá určitý prvek; naše metoda recursiveSum ()! Můžeme to nazvat znovu, ale změnit, který index sčítáme.

Předáváme ve stejném poli, které zpracováváme, ale předáváme další index z našeho aktuálního indexu. Děláme to jednoduše přidáním jednoho do našeho aktuálního indexu, jak je znázorněno.

Krok 6: Vytvořte pole celých čísel

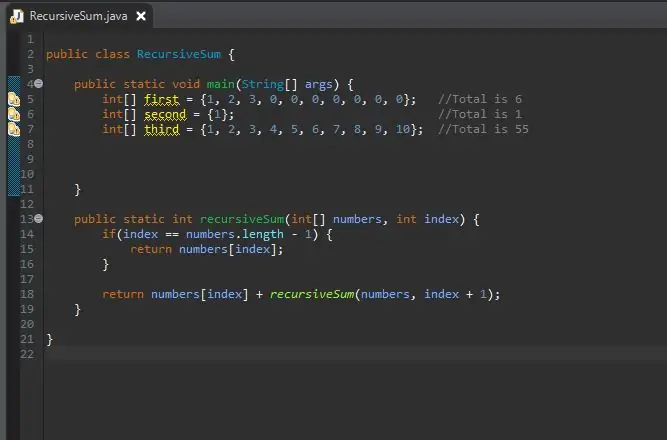
Nyní, když je naše rekurzivní metoda sčítání dokončena, můžeme vytvořit pole, které budeme zpracovávat. Toto pole bude v našem hlavním bloku metod.

Velikost pole můžete vytvořit tak dlouho, jak chcete. Vytvořil jsem několik různých polí s různými velikostmi a hodnotami, abych ukázal, že funguje nejen na jedné velikosti.

Krok 7: Zavolejte metodu svými poli

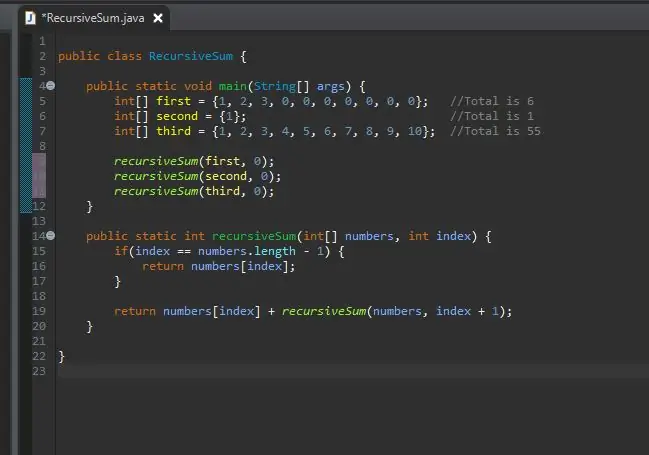
Nyní můžete zavolat rekurzivní metodu a předat jí tato pole. Nyní můžete spustit svůj program.

Krok 8: Vytiskněte výsledky

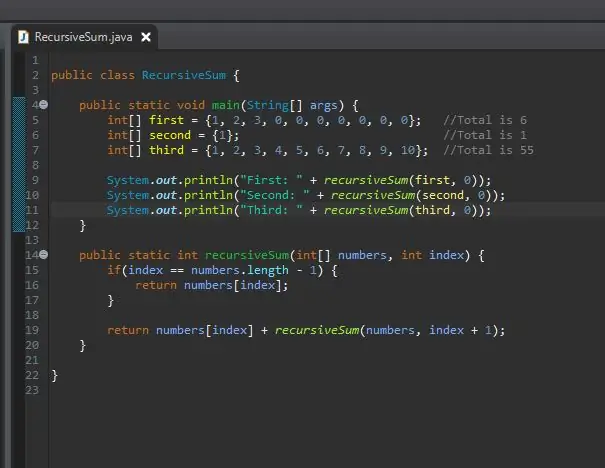
Se nic nestalo. Proč? Rekurzivní součet vrací celé číslo, ale s tímto celým číslem jsme nic neudělali. Své to udělalo, ale výsledek nevidíme. Abychom viděli výsledek, jednoduše jej vytiskneme. Po spuštění byste měli vidět výsledky pro všechna svá pole.

Krok 9: Gratulujeme

Dokončili jste rekurzivní funkci. Neváhejte změnit velikost svých polí. Pokud to vyzkoušíte, všimnete si, že se to zhroutí, když máte prázdné pole. Nezohlednili jsme to, ale je to skvělý způsob, jak zlepšit rekurzivní metodu.