
Obsah:
- Krok 1: Fotografujte
- Krok 2: Načtěte obrázky do MATLABu
- Krok 3: Analýza obrazu
- Krok 4: Vypočítejte šířku bílých čtverců na šachovnici
- Krok 5: Opakujte kroky 3 a 4 pro testovací obrázek
- Krok 6: Vypočítejte zvětšení objektivu
- Krok 7: Nalezení R-kvadrát a předpis uživatele pomocí interpolace
- Krok 8: Zobrazení předpisu uživatele na grafu
- Krok 9: Zúžte předpis
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:19.
- Naposledy změněno 2025-01-23 14:38.

Autor: Hannah Silos, Sang Hee Kim, Thomas Vazquez, Patrick Viste
Zvětšení je jednou z klíčových funkcí brýlí na čtení, které jsou klasifikovány podle předpisu dioptrií. Podle Michigan Technology University je dioptrie ohnisková vzdálenost čočky, obvykle měřená v mm, v jednotkách metrů (Michigan Technology University). Protože brýle na čtení mají konvexní čočky, ohnisková vzdálenost by byla kladná, což by způsobilo i dioptrie (HyperPhysics). Ohnisková vzdálenost se zvyšuje, jak se vzdálenost mezi objektem dostává dále od skutečné čočky, a to vede ke snižování dioptrií, protože jsou nepřímo úměrné. Mít brýle na čtení s dalšími dioptriemi by tedy pomohlo objektivu přiblížit pohled tak, že se může zdát, že ohnisková vzdálenost je menší zvýšením hodnoty dioptrií.
Uvedený kód bude použit k předpovědi dioptrie čočky s neznámým předpisem. Pro výpočet předpisu se používají dva vstupy: fotografie kontrolovaného pozadí bez použití jakýchkoli čoček a další fotografie stejného pozadí, ale prostřednictvím zvoleného objektivu. Program bude měřit zkreslení mezi těmito dvěma fotografiemi. Odtud budeme schopni odhadnout dioptrii objektivu a vytvořit výsledek, který si uživatel může prohlédnout.
K tomuto Instructable budete potřebovat:
- Černobílý šachovnicový vzor vytištěný na list papíru formátu 11x8,5
- Fotoaparát se schopností zablokovat zaostření
- Stativ nebo něco podobného k zajištění fotoaparátu
- Různé recepty na brýle na čtení
- MATLAB
Krok 1: Fotografujte



Abyste mohli vypočítat zvětšení čočky, musíte ji umět porovnat se skutečnou velikostí objektu. U tohoto projektu budeme porovnávat zvětšený obrázek s kontrolním obrázkem.
Prvním krokem je tedy pořízení dvou fotografií stejného obrázku - první pouze fotoaparátem a druhý objektivem brýlí na čtení, které chcete otestovat.
Pořídíte snímek černobílé šachovnice 8,5x11in s mřížkou 1in. Nastavte kameru 11 palců od šachovnice. Před pořízením fotografií uzamkněte zaostření na šachovnici.
Vyfoťte šachovnici bez brýlí na čtení. Poté, aniž byste cokoli pohnuli, umístěte brýle na čtení před fotoaparát a pořiďte druhou fotografii.
Dbejte na to, aby se poloha vaší kamery mezi záběry nepohybovala. Jediné, co by se mezi těmito dvěma fotografiemi mělo změnit, je přítomnost čočky brýlí před fotoaparátem.
Až budete s fotografiemi hotovi, nahrajte je do počítače.
Krok 2: Načtěte obrázky do MATLABu
Otevřete nový skript.
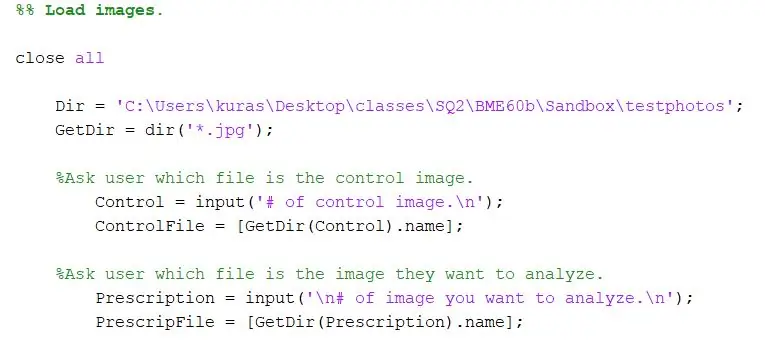
Nejprve určete adresář, kde jsou fotografie uloženy. Potom pomocí funkce dir extrahujte obrázky-j.webp
Dir = 'C: / Users / kuras / Desktop / classes / SQ2 / BME60b / Sandbox / testphotos'; GetDir = dir ('*. Jpg');
U našeho projektu jsme chtěli uživatele programu vyzvat, pro které soubory chce porovnat. V první části je uživatel požádán o zadání řídicího obrázku a ve druhé o zadání testovacího obrázku.
- %Zeptejte se uživatele, který soubor je řídicí obrázek.
- Control = vstup ('# kontrolního obrázku. / N');
- ControlFile = [GetDir (Control).name]
- %Zeptejte se uživatele, který soubor je obrázek, který chce analyzovat.
- ChooseFile = vstup ('\ n# obrázku, který chcete analyzovat. / N');
- PrescripFile = [GetDir (ChooseFile).name];
Krok 3: Analýza obrazu

Barevný obrázek v MATLABu má velikost MxNx3, zatímco obraz ve stupních šedi je MxN. To znamená, že je rychlejší vylepšit/upravit obrázek ve stupních šedi, protože je k dispozici méně dat, která je třeba sledovat. Pomocí nástroje rgb2gray převeďte obrázek na stupně šedi. (Byla použita funkce imrotate, protože naše fotografie byly horizontální - tento řádek kódu může nebo nemusí být ve vaší verzi nutný.)
- %převést na stupně šedi a otočit
- I = imread (ControlFile);
- I = rgb2gray (I);
- I = imrotovat (I, 90);
Dále zobrazte obrázek. Funkce subplot se používá k tomu, aby testovací obrázek mohl být v dalších krocích vedle ovládacího prvku.
- %Zobrazit
- Obrázek 1);
- podkres (1, 2, 1)
- imshow (I);
- název (ControlFile);
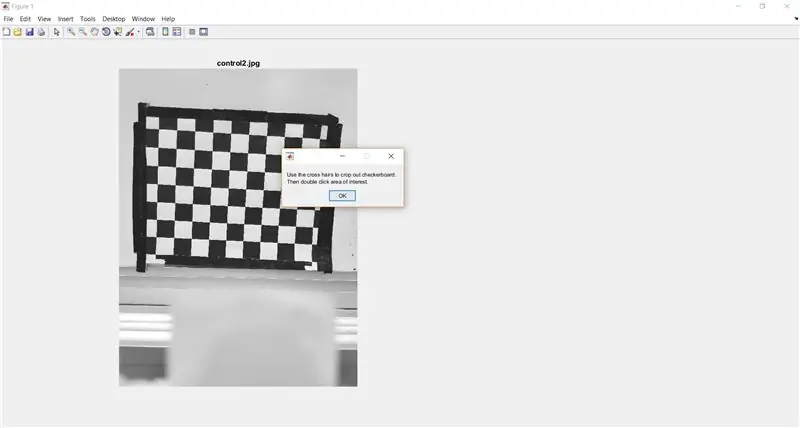
Pomocí příkazu imcrop vyzvěte uživatele, aby ořezal šachovnici z celého obrázku. Následující kód také ukazuje okno se zprávou, které má uživateli poskytnout pokyny.
- %výřez šachovnice pro analýzu
- waitfor (msgbox ({'Použijte křížové vlasy k oříznutí šachovnice.', 'Poté dvakrát klikněte na oblast zájmu.'}));
- I_crop = imcrop (I);
K binarizaci obrázku použijte imbinarize.
I_binary = imbinarize (I_crop);
Krok 4: Vypočítejte šířku bílých čtverců na šachovnici
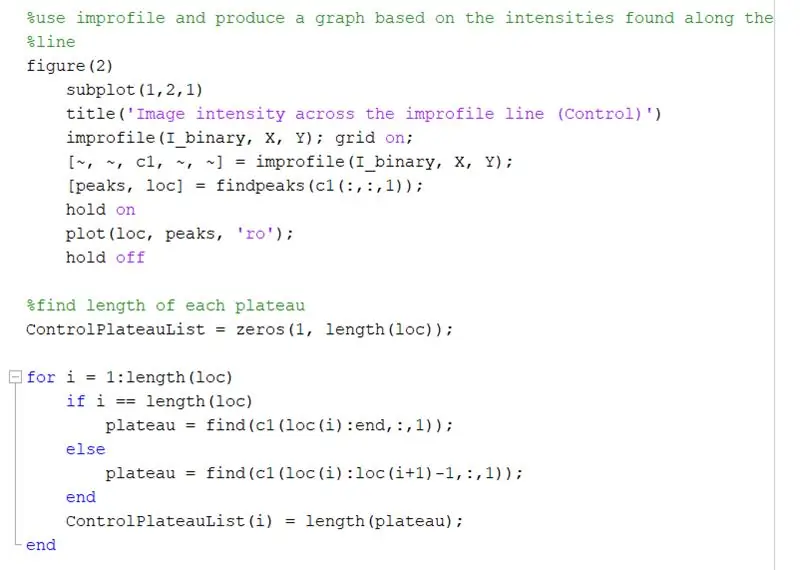
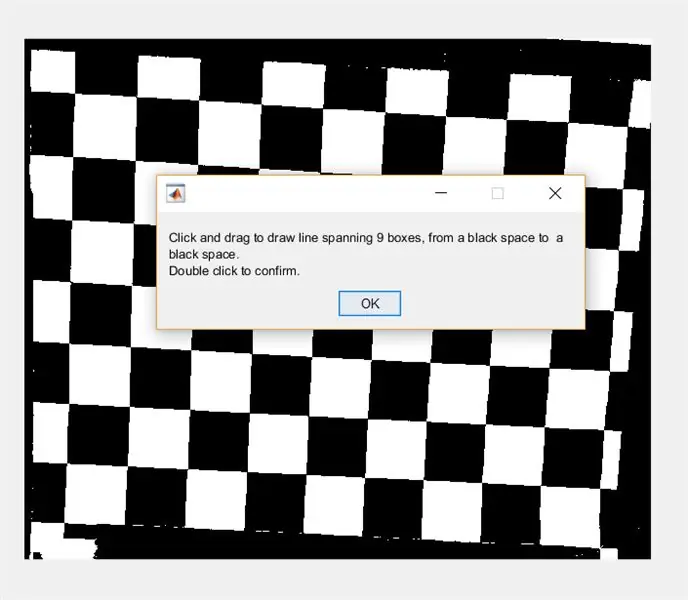
Dále vyzvěte uživatele, aby nakreslil čáru přes obrázek pomocí imline. Tato čára by měla probíhat vodorovně přes šachovnici. Mělo by začínat a končit na černém čtverci (nezáleží na tom, kde)- je to proto, že budeme měřit šířku bílých čtverců, nikoli černých.
- %rýsovací čára
- Obrázek 1)
- podkres (1, 2, 1)
- imshow (I_binary);
- waitfor (msgbox ({'Kliknutím a přetažením nakreslíte čáru o 9 polích, od černé mezery po černou mezeru.', 'Dvojitým kliknutím potvrdíte.'}));
- line = imline;
- pozice = čekání (řádek);
- koncové body = line.getPosition;
Extrahujte souřadnice X a Y pro koncové body nakreslené čáry.
- X = koncové body (:, 1)
- Y = koncové body (:, 2);
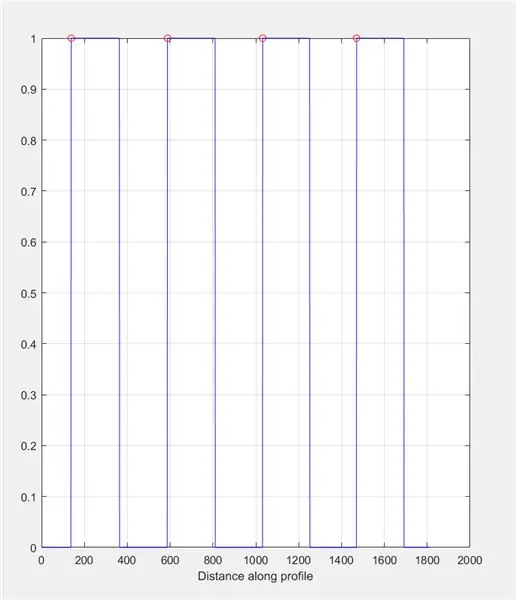
Použijte improfile k vytvoření grafu na základě intenzit nalezených podél nakreslené čáry. To by mělo připomínat čtvercovou vlnu v rozsahu od 0 (černá) do 1 (bílá). Vypočítejte také vrcholy a jejich umístění.
- obrázek (2)
- podkres (1, 2, 1)
- title ('Intenzita obrazu na řádku improfilu (ovládání)')
- improfile (I_binary, X, Y); mřížka zapnuta;
- [~, ~, c1, ~, ~] = neprofilní (I_binary, X, Y);
- [píky, loc] = findpeaks (c1 (:,:, 1));
- vydrž
- plot (loc, píky, 'ro');
- vydrž
Najděte délku každé plošiny na grafu neprofilu pomocí smyčky for. Spusťte smyčku for pro stejné množství vrcholů, jaké jsou v grafu neprofilu. Chcete -li vypočítat délku každé plošiny, použijte funkci „najít“a najděte všechna místa, kde je „1“namísto hodnoty intenzity „0“. Potom vypočítejte délku tohoto pole, abyste získali celkovou délku plošiny, která by se měla rovnat šířce bílého čtverce v pixelech. ControlPlateauList = nuly (1, délka (loc));
pro i = 1: délka (loc)
pokud i == délka (loc)
plateau = find (c1 (loc (i): end,:, 1));
jiný
plateau = find (c1 (loc (i): loc (i+1) -1,:, 1));
konec
ControlPlateauList (i) = délka (plošina);
konec
Krok 5: Opakujte kroky 3 a 4 pro testovací obrázek

*Poznámka: při kreslení neprofilové čáry na testovací obrázek ji nakreslete přes čtverce, které odpovídají čáře, kterou jste nakreslili na kontrolní obrázek.
Krok 6: Vypočítejte zvětšení objektivu

Zvětšená měření se vypočítají vydělením průměru délky plató, který byl vypočítán v kroku 5, průměrem délky kontrolního plató, který byl vypočítán v kroku 4. Toto je vypočteno jako 1,0884.
zvětšení = průměr (plateauList)/průměr (ControlPlateauList);
Krok 7: Nalezení R-kvadrát a předpis uživatele pomocí interpolace

Pomocí kódu:
- md1 = fitlm (GivenPrescription, MagArray);
- Rsquared = md1. Rsquared. Ordinary;
Můžeme najít R-druhou mocninu grafu GivenPresciption (hodnoty dané našimi čočkami) vs. MagArray (řada poměrů měření zvětšení, které jsme vypočítali dříve). Z dostatečně vysoké hodnoty R na druhou lze usoudit, že existuje dostatečně silná korelace, která ospravedlňuje použití této metody. V tomto konkrétním případě byla hodnota R na druhou 0,9912, což naznačuje silnou korelaci, a proto je použití této metody v analýze oprávněné.
Pomocí funkce:
Prescription = interp1 (MagArray, GivenPrescription, zvětšení, 'lineární');
Můžeme interpolovat odpovídající hodnotu předpisu (na ose x) našeho poměru zvětšení (hodnota na ose y) a zjistit, jaký je předpis uživatele.
Interpolace dat je důležitá pro to, aby tato metoda fungovala, protože nám umožňuje vytvářet předpoklady o informacích, které nemáme, na základě informací, které máme. Zatímco řada tohoto nejvhodnějšího řešení by byla technicky silnějším kandidátem pro tento předpoklad, vytváření hranic ke snížení počtu výstupů má stejný účinek, protože dioptrické brýle přicházejí každopádně v přírůstkových jednotných hodnotách. To je vysvětleno v dalších krocích.
Krok 8: Zobrazení předpisu uživatele na grafu

Pomocí následujícího kódu:
- postava;
- plot (GivenPrescription, MagArray, '-g')
- vydrž
- plot (předpis, zvětšení, 'bp')
- vydrž
- mřížka
- legenda ('Data', 'Interpolated Points', 'Location', 'NW')
Můžeme vykreslit graf, který ukazuje poměry zvětšení versus daný předpis se zelenou čarou a nalezená data našeho vypočítaného zvětšení versus náš interpolovaný předpis s modrou hvězdou. Poté legenda označí název, osu x a osu y a umístí legendu do levého horního rohu.
Krok 9: Zúžte předpis

K zaokrouhlení předpisu se používá následující kód:
-
pokud předpis <= 1,125
CalculatedPrescription = '1,0';
-
elseif Předpis <= 1,375
CalculatedPrescription = '1,25';
-
elseif Předpis <= 1,625
CalculatedPrescription = '1,5';
-
elseif Předpis <= 1,875
CalculatedPrescription = '1,75';
-
elseif Předpis <= 2,25
CalculatedPrescription = '2.0';
-
elseif Předpis <= 2,625
CalculatedPrescription = '2,5';
-
elseif Předpis <= 3
CalculatedPrescription = '2,75';
-
elseif Předpis <= 3,375
CalculatedPrescription = '3,25';
-
jiný
CalculatedPrescription = 'neznámý';
- konec
Předpis nalezený pomocí interpolace nemusí nutně odrážet skutečný předpis - je tomu tak proto, že v analýze fotografie v důsledku lidské chyby vždy dojde k mírným odchylkám. Tento krok tedy potřebujeme ke klasifikaci skutečného předpisu.
Předepsané předpisy obvykle začínají od 1,0 dioptrie a v předpisech se zvyšují o 0,25, takže po výpočtu předpisu chceme určit recept, který nejlépe vyhovuje tomu, co by uživatel mohl potřebovat. Po výpočtu předpisu provedeme danými příkazy If, abychom zkontrolovali jeho hodnotu a určili, který předpis je nezbytný. Cokoli menší nebo rovné 1,125, pak předpis je 1,0. Cokoli je menší než nebo rovno 1,375, předpis je 1,25. Cokoli menší než nebo rovné 1,625, předpis je 1,5. Cokoli menší nebo rovné 1,845, předpis je 1,75. A tak dále.
Hodnoty se zvyšují, protože kontrolujeme, zda jsou hodnoty menší než. Pokud bychom provedli snížení hodnot, pak by první if příkaz přečetl vždy první if příkaz. Pokud je předpis nejmenší, chceme, aby ho okamžitě rozpoznal jako nejmenší, a proto je nejmenší hodnota tím, čím jsme začali. Cokoli vyšší než nejvyšší hodnota znamená, že předpis není v rozsahu s našimi daty, zobrazí se tedy řetězec „Neznámý“.
Doporučuje:
Upozornění na vodu - zařízení, které zachrání vaši loď: 5 kroků (s obrázky)

Varování před vodou - zařízení, které zachrání vaši loď: Pokud jste majitelem lodi, je tu naprosté pohodlí, když konečně dostanete loď na suchou zemi. Nemůže se tam potopit. Všude jinde stojí před neustálou bitvou o překonání tendence sklouznout pod vlny a zmizet. Během zimy tady na Aljašce
Heartcrab: Lambada-Walking Robot ve vaší kapse!: 15 kroků (s obrázky)

Heartcrab: Lambada-Walking Robot in Your Pocket !: Toto je jeden z těchto projektů s více významy: je toto sýrový příbuzný " headcrabs " z videohry Half-Life? Možná chodící robot zamilovaný do berušky? Nebo beruška pilotuje svého vlastního mecha? Ať už je odpověď jakákoli
EYECOM - oční komunikátor: 3 kroky

EYECOM - Oční komunikátor: EYECON - Oční komunikátor pomáhá lidem se zdravotním postižením komunikovat, pomoc pro zdravotně postižené Je zaměřen na lidi, kteří nemohou mluvit a nemohou používat ruce. EYECOM používá Tobii Eye Tracker 4C za přibližně 160 EUR na skenování očí a software pro ovládání myši. Umět
Oční maska Spící hudba: 5 kroků

Eye Mask Sleeping Music: Toto je projekt, který vám umožní v noci lépe spát, spolehněte se na pomalou verzi vánoční písně o masce na oči
Retrofit LED žárovky pro Halo 998 Oční bulva: 8 kroků

Retrofit žárovky LED pro ozdobu oční bulvy Halo 998: Tento návod popisuje, jak upravit obruby oční bulvy Halo 998, aby bylo možné přijmout stmívatelnou žárovku LumiSelect PAR/R16 od earthled.com. Žárovka LED je příliš velká, aby se vešla otvorem v oční bulvě kousek, ale s trochou ef
