3D rekonstrukce z jedné fotografie: 8 kroků

2024 Autor: John Day | [email protected]. Naposledy změněno: 2024-01-30 08:18

Úloha 3D rekonstrukce je obvykle spojena s binokulárním viděním. Alternativně můžete kolem objektu přesunout jednu kameru. Mezitím, pokud je znám tvar předmětu, může být úkol vyřešen z jedné fotografie. To znamená, že máte pouze jednu kameru a nepohybuje se. Podívejme se, jak to udělat krok za krokem. Použijeme Rubikovu kostku, protože je dobře standardizovaná a má bohatou sadu funkcí. Lze jej považovat za velmi jednoduchý objekt a současně za komplikovanou konstrukci. Aby tedy strojové vidění splnilo úkol, musí překonat podstatné překážky.

Krok 1: Vyhodnoťte složitost úkolu

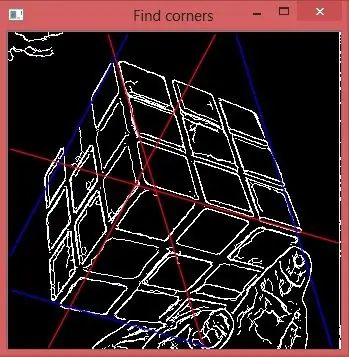
Na první pohled je úkol jednoduchý. Najděte centrální uzel, kde se spojí 3 hrany krychle, a nakreslete tyto hrany. Z jejich souřadnic je možné vypočítat vzdálenost od kamery a úhly otočení. Problém je, že tyto řádky neexistují. Z levého obrázku vidíte, že každý okraj je reprezentován 2 rovnoběžnými čarami. Kromě toho pravý horní obrázek ukazuje, že každý z nich je rozdělen na 3 segmenty. Navíc, pokud použijeme variantu populární Houghovy transformace, která dokáže detekovat úsečky, provede úlohu s některými chybami, které znemožňují detekci centrálního uzlu. Pokud se konce navzájem nedosáhnou, neexistuje jediný bod. Pokud detekce přestřelí konec, bude to vypadat jako uzel uprostřed okraje, jak vidíte na 2 zbývajících obrázcích.

Krok 2: Najděte správný přístup

Když příliš mnoho podrobností činí deterministické algoritmy nepoužitelnými, je na čase zvážit pravděpodobnostní přístup. Pokud vypočítáme zprůměrované parametry obrázku, jejich chyby se podstatně zmenší a metoda paradoxně dopadne spolehlivěji. Standardní transformace Hough nevytváří řádkové segmenty. Pouze jeho sklon theta a vzdálenost rho od počátku souřadnic. Tvoří část Houghova prostoru, která je zobrazena výše. Zde theta odpovídá vodorovné ose. Světlá místa označují možné čáry na obrázku. Všimněte si, že několik takových míst je umístěno nad sebou. Není divu, na našem obrázku je mnoho rovnoběžných čar. Mají stejnou thetu a různé rho.

Krok 3: Vypočítejte histogram Theta

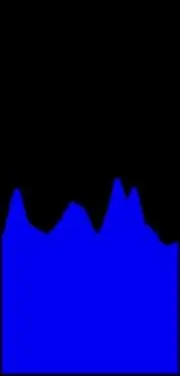
Pojďme detekovat takové klastry. Za tímto účelem shrneme hodnoty pro všechny tečky v prostoru Hough se stejnou theta. Na obrázku vidíte odpovídající histogram. Několik poznámek k měření. Když pracujete s obrázky v souřadnicích pixelů, osa X jde jako obvykle, ale Y ukazuje dolů, takže počátek souřadnic je v levém horním rohu a theta by měla být měřena od osy X ve směru hodinových ručiček. Mějte na paměti, že celý pohyb theta na obrázku je 180 stupňů, můžete přibližně zkontrolovat, zda 3 hlavní vrcholy představují 3 převládající svahy na obrázku.

Krok 4: Vypočítejte Rho histogram

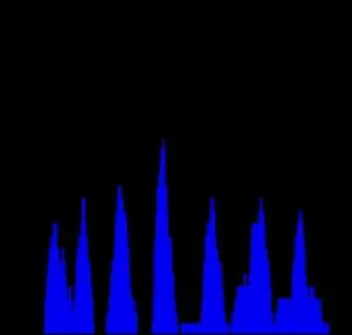
Nyní, když známe 3 hlavní shluky rovnoběžných čar, oddělme řádky v každém z nich. Stejný přístup můžeme zopakovat. Vezměme si sloupec z Houghova prostoru, který odpovídá jednomu píku na histogramu theta. Dále vypočítáme další histogram, kde osa X představuje hodnotu rho a Y - souhrnné hodnoty pro toto rho. Součet bude očividně menší, takže tento graf není tak hladký. Přesto jsou píky jasně viditelné a jejich počet (7) přesně odpovídá počtu rovnoběžných čar na zdrojovém obrázku. Bohužel ne všechny tabulky jsou tak dokonalé, ale princip je jasný.

Krok 5: Najděte centrální uzel

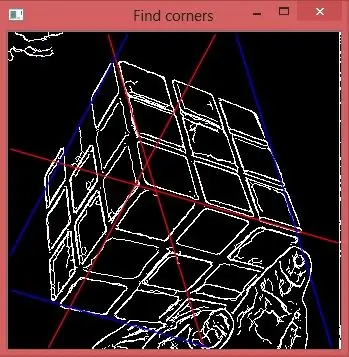
Pokud vezmeme centrální vrchol na histogramu rho pro každou thetu, získáme 3 řádky, které jsou na obrázku červené. Jejich křižovatka označuje nezbytný bod.

Krok 6: Vyberte si ze 2 alternativ

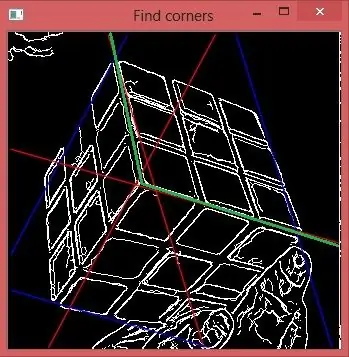
Vidíte, že každý řádek jde z centrálního bodu v obou směrech. Jak určit správnou polovinu? Vezměme si theta3. Předpokládejme, že vezmeme spodní část tohoto řádku. Vypočítáme další Houghův prostor pouze pro část obrázku od 2 zelených čar do pravého horního rohu obrázku. Poté pro něj vytvořte theta histogram. Vidíte, že třetí vrchol úplně zmizel, takže jsme udělali správnou volbu.

Krok 7: Určení vnějších rohů

Nyní můžeme použít první a poslední vrchol na histogramech rho, abychom nakreslili modré čáry, které oříznou červené okraje a označí zbývající rohy. Úkol je vyřešen.

Krok 8: Vyzkoušejte si to v praxi

Ilustrace pro tento Instructable byly vytvořeny pomocí Perception 1.0. Toto je bezplatný software, který používá OpenCV - výkonnou knihovnu pro počítačové vidění. Může být také spojen s WinNB, který byl použit v mém jiném Instructable, což poskytuje schopnost vidění pro robotiku. Oba programy si můžete stáhnout z nbsite. Pro instalaci stačí spustit stažený soubor exe. Později jej můžete odebrat pomocí standardního nástroje systému Windows. Stránka také obsahuje zdroje o počítačovém vidění a souvisejících tématech. V Perception najdete popsaný způsob 3D rekonstrukce i mnoho dalších. Výhodou tohoto programu je, že vydává konečný výsledek spolu s mezilehlými daty. Jste schopni zkoumat, jak funguje počítačové vidění, aniž byste byli programátorem. Pokud jde o zadávání, každá metoda má speciálně vybrané typické vzorky. Samozřejmě můžete použít i svůj vlastní. Je možné vkládat obrázky ze souboru nebo z kamery počítače. V případě jakýchkoli dotazů nebo návrhů mě neváhejte kontaktovat.