
Obsah:
- Krok 1: Shromážděte netištěné součásti
- Krok 2: 3D tisk modulu zrcadlového řízení
- Krok 3: Sestavte laserový modul
- Krok 4: Vytiskněte obojek laserového ukazovátka
- Krok 5: Sestavte hnací obvod
- Krok 6: Nahrajte ukázkový kód
- Krok 7: Snížení hlasitosti
- Krok 8: Ladění napětí za účelem snížení zkreslení
- Krok 9: Zdokonalení softwaru pomocí matematiky
- Krok 10: Nenákladný tester součástí zachraňuje den
- Krok 11: Najděte pružinovou konstantu K, vyřešte problém
- Krok 12: Otázky a odpovědi o obvodu ovladače pomocí diskrétních součástí
- Krok 13: Analýza aktuálních problémů a možná řešení
- Krok 14: Budoucí práce a možné aplikace
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:23.
- Naposledy změněno 2025-01-23 14:38.


V tomto Instructable budu demonstrovat konstrukci dvouosého, jednozrcadlového laserového paprskového řídicího modulu pomocí 3D tištěných dílů a levných komponent od eBay.
Tento projekt má podobnost s Arduino Laser Show s ovládáním Full XY a Arduino Laser Show s Real Galvos, ale věřím, že je první, kdo použil 3D tištěný design s levnými solenoidy. Všechny soubory návrhu vkládám pod GPLv3, aby bylo možné návrh vylepšit a vylepšit.
Ačkoli v současné době jsem pouze sestavil modul a napsal nějaký velmi základní testovací kód, doufám, že jednoho dne ho mohu posunout na další úroveň začleněním kódu vektorové grafiky z mého dřívějšího instruktovatelného, super rychlého analogového napětí od Arduina.
Krok 1: Shromážděte netištěné součásti
Laserová sestava se skládá z následujících částí:
- 4 mikro solenoidy
- Jedno 1/2 palcové zrcadlo
- Čtyři šrouby M3
Konkrétní solenoidy, které jsem použil, byly zakoupeny na eBay po 1,45 $ za kus. Kulaté zrcátko bylo nalezeno v řemeslné uličce v HobbyLobby - balíček 25 mě stál méně než 3 dolary. Zrcadla najdete také na eBay.
Budete také potřebovat levné laserové ukazovátko, opět z eBay. Fialový laser spolu se zářící vinylovou fólií je vynikající kombinací tohoto projektu!
Sada pomocných rukou není nutná, ale bude velmi užitečná pro držení a polohování laserového ukazovátka. K podržení tlačítka napájení lze použít velkou sponku na pořadač.
Budete potřebovat Arduino (použil jsem Arduino Nano) a způsob pohonu solenoidů. Jak VajkF uvedl v komentářích, můžete použít předem vyrobený H-můstek, jako jsou ty založené na L298 nebo L9110. Ty jsou k dispozici na eBay za pár dolarů a lze je použít také pro pohon motorů a robotických projektů.
Protože jsem neměl H-můstek, postavil jsem si vlastní ovladač z diskrétních komponent:
- Čtyři bipolární tranzistory NPN (použil jsem MPS3704)
- Čtyři odpory (použil jsem odpor 1,2 kOhm)
- Čtyři diody (použil jsem 1N4004)
- 9V baterie a konektor baterie
Elektronické součástky pocházely z mé laboratoře, takže na ně nemám přesné náklady, ale pokud už součástky nemáte nebo je můžete uklízet, je pravděpodobně nákladově efektivnější použít předem připravený H-můstek. Nicméně poskytnu schémata pro stavbu vlastních.
Krok 2: 3D tisk modulu zrcadlového řízení
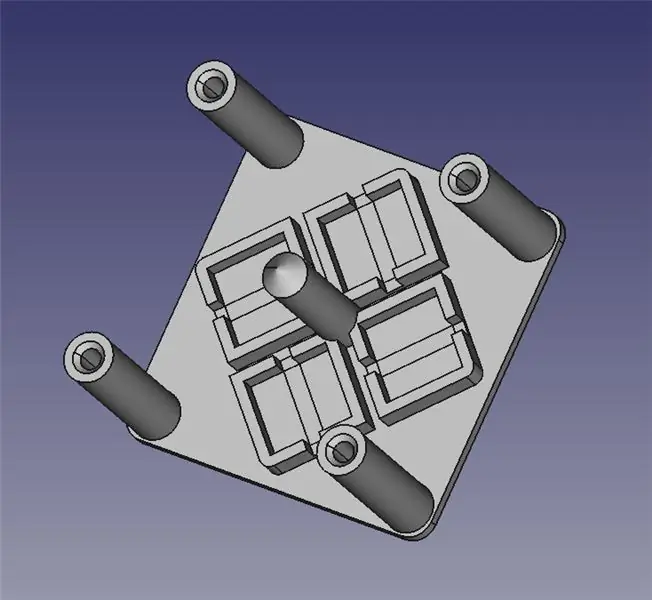
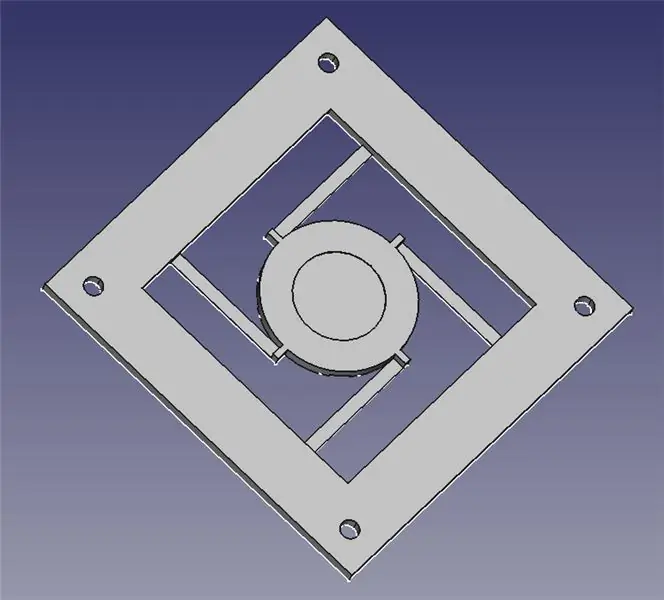
Modul laserového řízení se skládá ze dvou 3D tištěných částí: základny pro montáž čtyř solenoidů a kloubové plošiny pro zrcátko.
Připojil jsem pro vás dva soubory STL k 3D tisku a také soubory FreeCAD pro případ, že potřebujete upravit design. Veškerý obsah spadá pod GPLv3, takže svá vylepšení můžete provádět a sdílet!
Krok 3: Sestavte laserový modul



- Pomocí horkého lepidla připevněte čtyři solenoidy ke spodnímu dílu.
- Pomocí horkého lepidla připevněte zrcátko na střed horního dílu.
- Vložte kovové písty do solenoidů a poté umístěte horní díl na sloupky (ale nešroubujte jej). Mírně otočte horní kus a pomocí malého šroubováku zvedněte každý píst do polohy. Okraj kotouče by měl sklouznout do drážky na pístu. Buďte opatrní, protože 3D tištěné závěsy jsou velmi křehké. S trpělivostí a možná s několika neúspěšnými pokusy byste měli být schopni umístit všechny čtyři písty bez kroucení nebo vyvíjení tlaku na závěsy.
- Jakmile jsou všechny písty umístěny, částečně zasuňte šrouby M3, ale před jejich utažením jemně zatlačte na každý píst dolů a ujistěte se, že se zrcátko volně naklání. Pokud se nepohybuje volně nebo se zachytává, může být nutné sejmout horní desku, uvolnit jeden nebo více solenoidů a znovu ji připevnit v mírném vnějším úhlu (v tomto může pomoci umístění mezikusů mezi ní a středový sloupek).
Krok 4: Vytiskněte obojek laserového ukazovátka
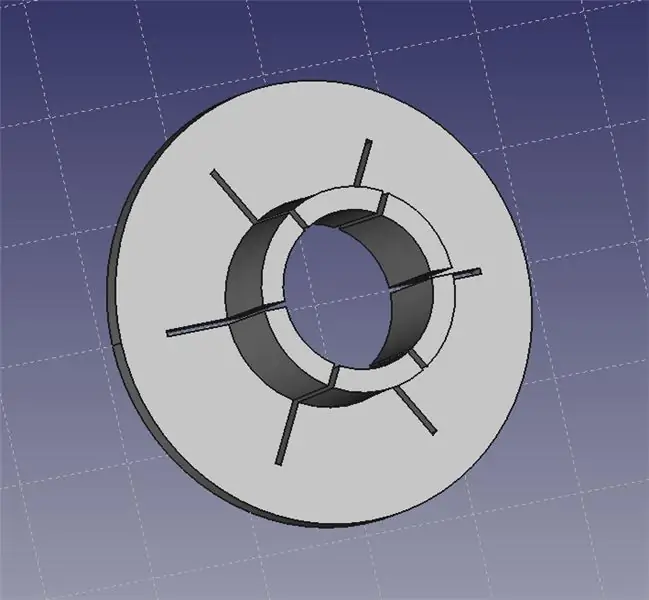

Obojek laserového ukazovátka pasuje na hlavu laserového ukazovátka. Poté můžete pomocí sady pomocných rukou uchopit límec a umožnit vám přesné umístění laseru na lavici.
Krok 5: Sestavte hnací obvod
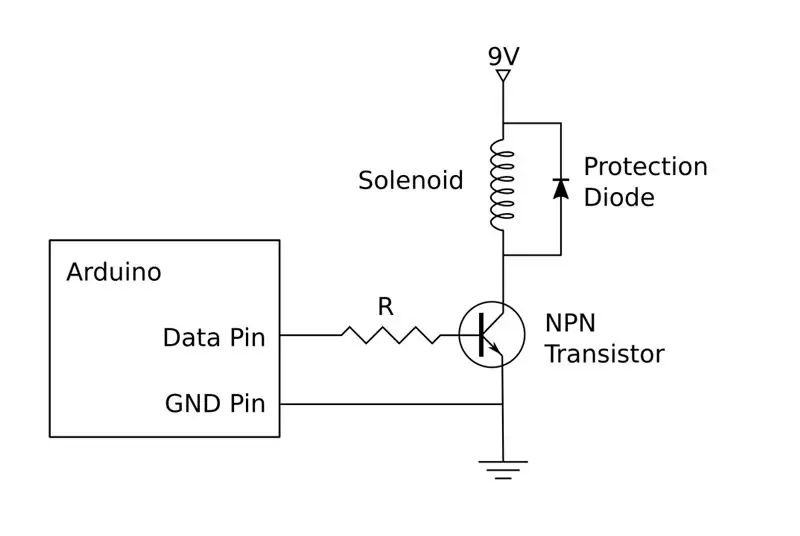
Obvod pohonu je znázorněn na schématu. Jak již bylo řečeno, moje verze je postavena na diskrétních komponentách, ale můžete také použít snadno dostupný H-můstek. Pokud se rozhodnete postavit vlastní, budete muset postavit čtyři kopie tohoto obvodu, jednu pro každý ze čtyř solenoidů.
Každý obvod se připojí k pinu Arduino, dva pro ovládání levého a pravého solenoidu a dva pro solenoidy nahoru a dolů. Ty budou muset být připojeny k pinům podporujícím PWM, například:
- Pin 9: Solenoid nahoru
- Pin 3: Down solenoid
- Pin 11: Levý solenoid
- Pin 10: Pravý solenoid
Jednu 9V baterii lze použít k napájení všech čtyř obvodů budiče elektromagnetu nebo můžete použít stolní napájecí zdroj. Arduino vybije USB a nemělo by být připojeno k kladné straně 9V baterie. Záporná strana baterie se však používá jako referenční uzemnění a měla by být připojena ke kolíku GND na Arduinu i ke kolíkům emitorů na tranzistorech.
Krok 6: Nahrajte ukázkový kód

Ukázkový kód byl aktualizován s následujícími funkcemi:
- Upravuje frekvenci PWM tak, aby byl mechanismus při nízkých rychlostech téměř tichý. Bzučení v testu pohybu 1 úplně zmizelo!
- Přidá jako napěťové rovnice na základě Schimpfova článku za účelem „linearizace“nelineární odezvy solenoidů.
Také jsem zahrnul implementaci Lorenz Attractor na základě kódu z tohoto blogu.
Věrnost výsledků je docela žádoucí, ale stále na tom pracuji!:)
Následující kroky ilustrují některé z technik použitých v kódu.
Krok 7: Snížení hlasitosti
V mém testu pohybu 1 můžete slyšet hlasité bzučení, zejména při pohybu nahoru a dolů. Ukazuje se, že to bylo způsobeno tím, že výchozí frekvence sekání PWM Arduina je ve slyšitelném rozsahu. Rychlé zapínání a vypínání napětí cívky by způsobilo, že vibrují na této frekvenci, což z nich udělá malé malé reproduktory.
Abych tento problém vyřešil, zvýšil jsem v kódu frekvenci PWM:
#define PWM_FREQ_31372Hz 0x01 // Nastaví frekvenci PWM na 31372,55 Hz #definuje PWM_FREQ_3921Hz 0x02 // Nastaví frekvenci PWM na 3921,16 Hz #define PWM_FREQ_980Hz 0x03 // Frekvence PWM & 0b11111000) | frekvence; // Nastavit frekvenci timer1 (piny 9 a 10) TCCR2B = (TCCR2B & 0b11111000) | frekvence; // Nastavit frekvenci timer2 (piny 3 a 11)}
Nastavení frekvence PWM Arduino je užitečný trik pro utlumení elektromagnetů nebo motorů. Experimentujte s různými možnostmi frekvencí, abyste zjistili, která vám poskytne nejlepší výsledky. Ačkoli to zahrnuje nějaké pokročilejší programování, dobrý zdroj o tom, jak fungují časovače, je zde.
Krok 8: Ladění napětí za účelem snížení zkreslení

Moje počáteční pohybové testy ukázaly, že došlo k významnému zkreslení reakce solenoidů. V testu pohybu 3 (obrázek vlevo) se místo toho měla stát kruhovou spirálou obdélníková pavučina se zubatými okraji.
Řešení tohoto problému vyžadovalo trochu matematiky, ale dokázal jsem na webu najít úžasný papír, který mi pomohl problém dostatečně dobře pochopit, abych jej vyřešil softwarově.
To, co následuje, vás provede procesem, kterým jsem prošel vyladěním systému a zlepšením vzhledu výsledných stop!
Krok 9: Zdokonalení softwaru pomocí matematiky
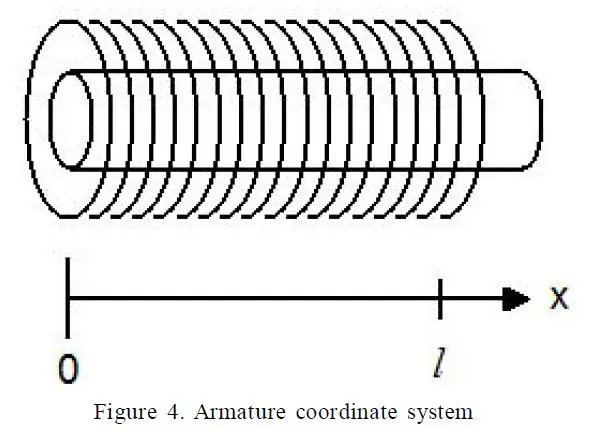
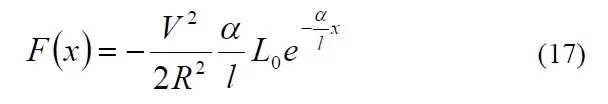
Tajemstvím vyladění systému se ukázal být výborný dokument nazvaný „Podrobný vysvětlení solenoidové síly“od Paula H. Schimpfa z Eastern Washington University (odkaz). Zejména rovnice 17 mi dala solenoidovou sílu z hlediska různých výrazů.
Následující termíny bylo snadné měřit:
- R - Odpor mého solenoidu
- l - Délka solenoidu
- x - Posun pístu v solenoidu
- V - Napětí na solenoidu
Také jsem věděl, že síla vyvíjená solenoidem musí vyvážit sílu z 3D tištěných pružin na dvouosém zrcadle. Síla pružiny se řídí Hookeovým zákonem, který je uveden následovně:
F = -kx
Přestože jsem neznal hodnotu k, alespoň jsem věděl, že síla, kterou jsem dostal z rovnice 17 ze Schimpfova papíru, se musí rovnat síle z Hookeova zákona.
Hodnota alfa (α) byla složitá. Ačkoli rovnice 13 a 14 ukázaly, jak vypočítat tyto hodnoty z oblasti solenoidu (A), počtu závitů (N) a hodnot magnetické permeability (μ), nechtěl jsem roztrhat solenoid, abych spočítal počet závitů, ani jsem neznal materiál, ze kterého bylo vyrobeno jádro mého solenoidu.
Krok 10: Nenákladný tester součástí zachraňuje den

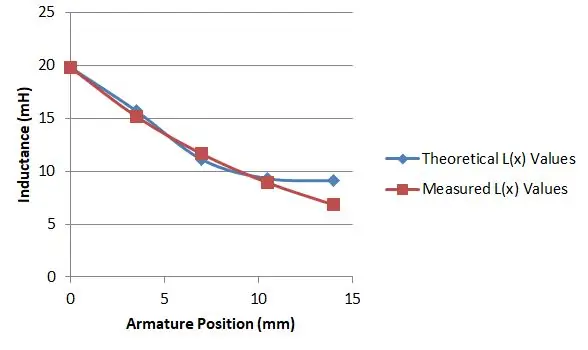

Ukázalo se však, že rovnice 15 a 16 mi dala to, co jsem potřeboval. Měl jsem levný tester komponent M328, který jsem koupil od eBay za 10 $. Dokázal to použít k měření indukčnosti mého solenoidu a zjistil jsem, že zatlačením kotvy dovnitř různých hloubek jsem získal různé indukční hodnoty.
Měření s plně zasunutou kotvou mi dalo hodnotu L (0).
Délka mého solenoidu byla 14 mm, takže jsem změřil indukčnost s kotvou v pěti polohách a to mi dalo různé hodnoty pro L (x):
- L (0,0) = 19,8 mH
- L (3,5) = 17,7 mH
- L (7,0) = 11,1 mH
- L (10,5) = 9,3 mH
- L (14) = 9,1 mH
Potom jsem použil tabulku k vykreslení svých hodnot vs. hodnoty rovnice 15 a 16 pro konkrétní volbu μr a poté jsem svou volbu obměňoval, dokud jsem nenašel dobrou shodu. To se stalo, když μr bylo 2,9, jak ukazuje graf.
Krok 11: Najděte pružinovou konstantu K, vyřešte problém
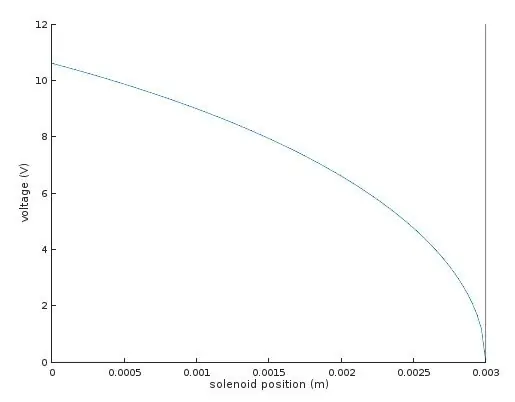

Jedinou zbývající neznámou byl K, pružinová konstanta. Změřil jsem to tak, že jsem na jeden ze solenoidů v mé dvouosé sestavě použil 9V a změřil vzdálenost, ve které bylo zrcátko staženo. S těmito hodnotami jsem byl schopen vyřešit rovnice pro K, které jsem našel kolem 10,41.
Nyní jsem měl hodnoty, které jsem potřeboval pro výpočet tahu solenoidu v různých polohách podél zdvihu. Nastavením F (x) rovnajícím se síle pružiny z Hookeova zákona mohu vyřešit požadované napětí V.
Graf ukazuje napětí potřebné pro pohyb solenoidu do libovolné požadované polohy x.
Vpravo, kde je napětí nulové a poloha 3 mm, to odpovídá neutrálnímu klidovému bodu solenoidu, když jsou 3D tištěné závěsy plně uvolněné. Pohyb doleva na grafu odpovídá zatažení kotvy do solenoidu proti tahu 3D tištěných závěsů-to zpočátku vyžaduje větší napětí, ale jak se kotva dostává hlouběji do solenoidu, tah se zvyšuje a požadované napájecí napětí se zužuje.
Tento vztah je rozhodně nelineární, ale s rovnicemi z Schimpfova článku mohu napsat svůj kód Arduino pro výstup správných napětí, takže průhyb paprsku je lineární:
float positionToVoltage (float x) {
// Obnovující síla působící závěsy (Hookův zákon) na požadované x. const float spring_F = -pramen_K * (x - jaro_X0); // Napětí takové, aby se tažná síla solenoidu shodovala s // obnovovací silou vratných kloubů sqrt (-2*R*R*(-spring_F)*solenoid_len/(a*L_0*exp (-a*x/solenoid_len)))); }
To vede k mnohem kruhovější spirále než v mém původním testu pohybu. Mise splněna!
Krok 12: Otázky a odpovědi o obvodu ovladače pomocí diskrétních součástí
Proč nemohu připojit solenoid přímo k Arduinu?
Jde o to, jaký proud dokáže Arduino poskytnout, aniž by utrpěl poškození. To je asi 40 mA na pin. S vědomím, že Arduino pracuje na 5V, můžeme použít Ohmův zákon k výpočtu požadovaného minimálního odporu zátěže (v tomto případě solenoidu). Rozdělení 5 voltů o 0,040 ampérů nám dává 125 ohmů. Pokud má zátěž větší odpor, můžeme ji připojit přímo k Arduinu, jinak ne. Malý solenoid má obvykle odpor 50 ohmů, takže jej nemůžeme řídit přímo z Arduina. Pokud bychom to udělali, vytáhlo by to 100mA, což je zjevně příliš.
Proč používáte 9V pro solenoid, ale 5V pro Arduino?
Arduino běží na 5V, ale to je na solenoid trochu málo. Použití tranzistoru nám umožňuje vybrat napětí pro solenoid, které je nezávislé na 5V použitém pro Arduino.
Jak poznám, zda je pro tento projekt vhodný tranzistor?
Stejně jako Arduino je hlavním požadavkem, aby proud protékající solenoidem nepřekročil maximální hodnocení pro tranzistor (zejména kolektorový proud). Můžeme snadno vypočítat nejhorší scénář měřením odporu solenoidu a poté rozdělením napájecího napětí. V případě napájecího proudu 9 V pro solenoidy a odporu solenoidu 50 ohmů nás nejhorší scénář uvádí na 180 mA. Například MPS3704 je dimenzován na maximální kolektorový proud 600 mA, což nám dává rozpětí asi 3.
Jak zjistím minimální hodnotu odporu mezi výstupem Arduina a základnou tranzistoru?
Výstup Arduina spojí základní nohu bipolárních tranzistorů přes odpor omezující proud. Protože Arduino pracuje na 5V, můžeme opět použít Ohmův zákon k výpočtu odporu potřebného k omezení proudu pod 40mA. To znamená, že rozdělte 5 voltů o 0,04 ampérů, abyste získali hodnotu alespoň 125 ohmů. Vyšší hodnoty odporu sníží proud, což nám poskytne ještě větší bezpečnostní rezervu.
Existuje pro tento odpor maximální hodnota, kterou bych neměl překročit?
Ukázalo se, že ano. Tranzistor má to, co je známé jako proudový zisk. Pokud je například zisk 100, znamená to, že pokud vložíme 1mA do základny, pak až 100mA bude proudit zátěží, kterou tranzistor ovládá. Pokud do základny vložíme 1,8 mA, pak zátěží protéká až 180 mA. Protože jsme dříve počítali, že při 9V protéká solenoidem 180mA, pak je „sweet spot“základní proud 1,8mA a méně a náš solenoid se nezapne úplně.
Víme, že Arduino vydává 5 V a chceme, aby protékal proud 1,8 mA, takže pro výpočet odporu (R = V/I) používáme Ohmův zákon (R = V/I). 5V děleno 1,8mA dává odpor 2777 ohmů. Takže vzhledem k předpokladům, které jsme učinili, očekáváme, že odpor se bude pohybovat mezi 125 a 2777 - volba něčeho jako 1000 ohmů nám dává v každém případě docela dobrou bezpečnostní rezervu.
Krok 13: Analýza aktuálních problémů a možná řešení

Současný prototyp ukazuje potenciál, ale stále existuje několik problémů:
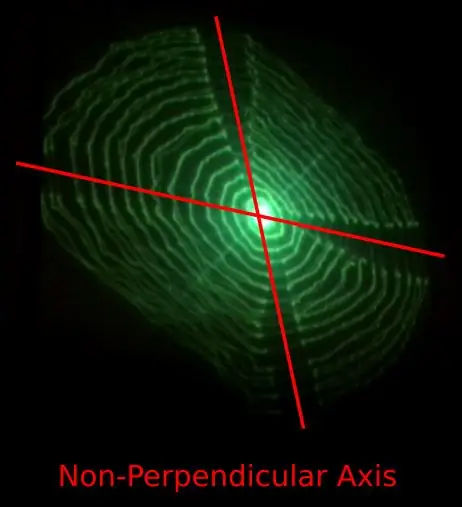
- Pohyb podél osy X a Y se nezdá být kolmý.
- Když zrcadlo změní směr, dojde ke skoku.
- Rozlišení je poměrně nízké a jsou zde viditelné schody schodišťových stupňů.
- Při vyšších rychlostech pohybu je dráha laseru zkreslena vibracemi a zvoněním.
Problém 1) může být způsoben konstrukcí 3D tištěných pružných závěsů, které přenášejí pohyb podél jedné osy na kolmou osu.
Problém 2) je způsoben vůlí ve spojce mezi hnacími písty a platformou zrcátek, což způsobuje, že zrcátko trhne a přeskočí při přechodech mezi osou X a Y. Tento náhlý pohyb vede k zatemněné mezerě ve tvaru X, kde laserová tečka provádí rychlejší nekontrolovaný pohyb.
Problém 3) nastává, protože výchozí Arduino PWM má pouze 255 úrovní a několik z nich je zbytečných kvůli tvaru křivky napětí. To lze výrazně zlepšit použitím časovače1, který má 16 bitů a byl by schopen 65536 unikátních hodnot.
Problém 4) nastává, protože zrcátko a kluzná kotva solenoidu (písty) představují značné množství pohybující se hmoty.
Protože problémy 1) a 2) souvisejí s mechanickou konstrukcí, jednou z možností může být odstranění kovových pístů a jejich nahrazení malými magnety vzácných zemin, které jsou připevněny přímo na naklápěcí desku. Solenoidy by byly otevřenou cívkou, která by přitahovala nebo odpuzovala magnety bez fyzického kontaktu. To by vedlo k plynulejšímu pohybu a vyloučení možnosti trhnutí a snížení celkové hmotnosti.
Snížení hmotnosti je primárním řešením pro problém 4), ale všechny zbývající problémy by mohly být zaměřeny přímo v softwaru implementací profilu řízení pohybu v softwaru za účelem zrychlení a zpomalení zrcadla kontrolovaným způsobem. To je již široce prováděno ve firmwaru 3D tiskárny a podobné metody mohou fungovat i zde. Zde je několik zdrojů souvisejících s řízením pohybu, které platí pro 3D tiskárny:
- „Matematika profilů řízení pohybu“, Chuck Lewin (odkaz)
- „Jerk Controlled Motion Explained“, (odkaz)
Mám podezření, že přidání lichoběžníkového profilu řízení pohybu by umožnilo řídit zrcátko mnohem vyšší rychlostí bez vyzvánění nebo vibračních artefaktů.
Krok 14: Budoucí práce a možné aplikace
Přestože vývoj řešení těchto problémů bude vyžadovat značné množství práce, doufám, že se tento modul řízení paprsků s otevřeným zdrojovým kódem může stát dostupnou alternativou projektů založených na galvanometru v takových aplikacích, jako jsou:
- Levná laserová show pro DJ a VJ.
- Elektromechanický vektorový displej pro vintage arkádovou hru, jako je Vectrex.
- 3D tiskárna SLA 3D typu pryskyřice, která v duchu pohybu RepRap dokáže vytisknout vlastní modul laserového řízení.
- Digitální posouvání nebo optická stabilizace obrazu u kamer.


Druhá cena v Arduino Contest 2017
Doporučuje:
Řídicí modul PSP přepínače Raspberry Pi ATX: 3 kroky

Řídicí modul přepínače Raspberry Pi ATX PSU: V systému složeném z RaspberryPi napájeného napájecím zdrojem ATX je cílem tohoto obvodu umožnit zapnutí nebo vypnutí systému jediným tlačítkem. Tento tutoriál byl vyvinut podle sitelec.org
Vytvořte řídicí panel počasí pomocí API Dark Sky: 5 kroků (s obrázky)
Build a Weather Dashboard using Dark Sky API: Dark Sky se specializuje na předpověď počasí a vizualizaci. Nejúžasnějším aspektem Dark Sky je jejich počasí API, které můžeme použít k načtení údajů o počasí téměř odkudkoli na světě. Nejde jen o deštivé nebo slunečné počasí, ale také o temperament
Zabezpečení SCADA pro řídicí systémy založené na Arduinu: 5 kroků

Zabezpečení SCADA pro řídicí systémy založené na Arduinu: SCADA (Supervisory Control and Data Acquisition) je rámec pro monitorování a vzdálený přístup k řídicím systémům běžně používaným v celé řadě průmyslových systémů, jako jsou elektrárny, železnice, výrobní jednotky, ocelárny, letadla , s
Řídicí jednotka počítače: 10 kroků (s obrázky)

Řídicí jednotka počítače: Zdravím všechny! Vytvořil jsem toto pole pro " vylepšení " můj počítač, s ním můžete přepínat připojení k internetu, zvukový výstup a vstup pro mikrofon. Můžete také zapnout a vypnout každého fanouška počítačové skříně a ovládat jeho rychlost, i když
SCADA pro řídicí systémy založené na Arduinu: 5 kroků

SCADA pro řídicí systémy založené na Arduinu: SCADA (Supervisory Control and Data Acquisition) je rámec pro monitorování a vzdálený přístup k řídicím systémům běžně používaným v celé řadě průmyslových systémů, jako jsou elektrárny, železnice, výrobní jednotky, ocelárny, letadla a
