
Obsah:
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:19.
- Naposledy změněno 2025-01-23 14:38.


Měření frekvence ze zachyceného signálu může být obtížný úkol, zejména na Arduinu, protože má nižší výpočetní výkon. Existují metody k zachycení přechodu nuly, kde je frekvence zachycena kontrolou, kolikrát signál překročí nulové čáry v daném čase. Taková metoda nemusí fungovat, pokud je signál kombinací různých frekvencí.
To je nějak obtížné kódovat, pokud nejste z takového pozadí. Ale jako drobet může být tento kód velmi užitečný pro různé projekty týkající se hudby, analýzy signálu. Motivem tohoto projektu bylo připravit kód, který lze na Arduinu snadno implementovat, aniž byste se dostali do pozadí.
Tento projekt nevysvětluje fungování FFT, ale vysvětluje použití funkce FFT. Stejný postup je také vysvětlen v přiloženém videu.
Pokud vás zajímá pouze aplikace kódu, a ne jeho vysvětlení. Můžete přeskočit přímo na krok č. 3.
Krok 1: Úvod do frekvenční transformace


Jakýkoli signál může být složen z kombinace různých sinusových vln. Takže jakýkoli časový signál může být také ukázán jako kombinace různých sinusů různých amplitud.
Pokusil jsem se vysvětlit fungování DFT (diskrétní Fourierova transformace) v jednom z předchozích instrukovatelných (https://www.instructables.com/id/Arduino-Frequency…). Tyto metody jsou extrémně pomalé pro všechny aplikace v reálném čase. díky čemuž je téměř k ničemu.
Na obrázku je zobrazen signál, který je kombinací dvou frekvencí f2 a f5. Tento signál je vynásoben testovacími sinusovými vlnami hodnot f1 až f5.
Matematicky lze ukázat, že -součet násobení dvou harmonických datových sad s různou frekvencí má tendenci k nule (vyšší počet dat může vést k výsledku těsta). V našem případě, pokud má tato dvě frekvence násobení stejnou (nebo velmi blízkou) frekvenci, je součet násobení nenulové číslo.
Pokud je tedy náš signál vynásoben f1, součet násobení bude nulový (pro skutečnou aplikaci téměř nulový). podobné je to u f3, f4. Pro hodnotu však výstup f2 a f5 nebude nulový, ale výrazně vyšší než ostatní hodnoty.
Zde je signál testován s 5 frekvencemi, takže signál je třeba vynásobit pěti frekvencemi. Tak intenzivní výpočet trvá déle. Matematicky je ukázáno, že pro N počet vzorků je zapotřebí N*N komplexní násobení.
Krok 2: Rychlá Fourierova transformace
Aby byl výpočet DFT rychlejší, vyvinuli algoritmus FFT James Cooley a John Tukey. Tento algoritmus je také považován za jeden z nejdůležitějších algoritmů 20. století. Rozděluje signál na lichou a sudou sekvenční část, což snižuje počet požadovaných výpočtů. Jeho použitím lze celkové požadované komplexní násobení snížit na NlogN. což je výrazné zlepšení.
Níže můžete odkazovat odkazy, na které jsem odkazoval při psaní kódu pro podrobné pochopení matematiky za FFT:
1.
2.
3.
4.
Krok 3: Vysvětlení kódu
1. Rychlý sinus a kosinus:
Výpočet FFT bere hodnotu různých sinusů a kosinů několikrát. Vestavěná funkce Arduina není dostatečně rychlá a poskytnutí požadované hodnoty zabere hodně času. Díky tomu je kód výrazně pomalejší (zdvojnásobuje čas u 64 vzorků). Abychom tomuto problému zabránili, je hodnota sinus pro 0 až 90 stupňů uložena jako násobek 255. Tím se odstraní potřeba používání čísel jako float a můžeme je uložit jako byte, který zabírá 1/4 prostoru na Arduinu. Sine_data musí být vložen na začátek kódu, aby byl deklarován jako globální proměnná.
Kromě sine_data je pole s názvem f_peaks deklarováno jako globální proměnná. Po každém spuštění funkce FFT se toto pole aktualizuje. Kde f_peaks [0] je nejdominantnější frekvence a další hodnoty v sestupném pořadí.
byte sine_data [91] = {0, 4, 9, 13, 18, 22, 27, 31, 35, 40, 44, 49, 53, 57, 62, 66, 70, 75, 79, 83, 87, 91, 96, 100, 104, 108, 112, 116, 120, 124, 127, 131, 135, 139, 143, 146, 150, 153, 157, 160, 164, 167, 171, 174, 177, 180, 183, 186, 189, 192, 195, 198, 201, 204, 206, 209, 211, 214, 216, 219, 221, 223, 225, 227, 229, 231, 233, 235, 236, 238, 240, 241, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 253, 254, 254, 254, 255, 255, 255, 255}; float f_peaks [5];
Protože máme uloženou hodnotu sinu pro 0 až 90 stupňů, lze vypočítat jakoukoli hodnotu sinu nebo kosinu. Níže funguje první kolo čísla s nulovou desetinnou čárkou a návratová hodnota z uložených dat. tato metoda potřebuje pouze jedno plovoucí dělení. To lze dále snížit přímým ukládáním hodnot sinusů (ne 255 násobků). ale to pohlcuje vysokou paměť na Arduinu.
Použití výše uvedeného postupu snižuje přesnost, ale zvyšuje rychlost. Pro 64 bodů dává výhodu 8 ms a pro 128 bodů dává výhodu 20 ms.
Krok 4: Vysvětlení kódu: Funkce FFT
FFT lze provést pouze pro velikost vzorku 2, 4, 8, 16, 32, 64 atd. pokud hodnota není 2^n, pak bude mít spodní stranu hodnoty. Pokud například vybereme velikost vzorku 70, pak bude brát v úvahu pouze prvních 64 vzorků a vynechá zbytek.
Vždy se doporučuje mít velikost vzorku 2^n. který může být:
2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, …
Dva plováky out_r a out_im zaberou velké množství paměti. pro Arduino nano nebude fungovat pro vzorky vyšší než 128 (a v některých případech 128) kvůli nedostatku dostupné paměti.
data bez znaménka [13] = {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048};
int a, c1, f, o, x; a = N; for (int i = 0; i <12; i ++) // výpočet úrovní {if (data <= a) {o = i;}} int in_ps [data [o] = {}; // vstup pro sekvenování float out_r [data [o] = {}; // skutečná část transformace float out_im [data [o] = {}; // imaginární část transformace
Další tok je následující:
1. Kód generuje bitové obrácené pořadí pro danou velikost vzorku (podrobnosti o bitovém obrácení na referencích: krok 2)
2. Vstupní data seřazená podle vygenerované objednávky, 3. FFT provedeno
4. Vypočítaná amplituda komplexního čísla, 5. Píky jsou detekovány a seřazeny sestupně
6. výsledky jsou přístupné z f_peaks.
[pro přístup k dalším datům (kromě špičkové frekvence) by měl být upraven kód, aby bylo možné lokální proměnnou zkopírovat do nějaké předdefinované globální proměnné]
Krok 5: Testování kódu


Jako vstup je uveden vzorek trojúhelníkové vlny. pro tuto vlnovou vzorkovací frekvenci je 10 Hz a samotná frekvence vlny je 1,25 Hz.
Jak je patrné ze surového výstupu, hodnota odpovídá FFT vypočítanému Scilabem. tyto hodnoty však nejsou úplně stejné jako my s nízkou přesností, ale rychlejší sinusová vlna.
Ve výstupní frekvenci je frekvence pole 1,25 a 3,75. není nutné pokaždé získat přesnou hodnotu. obvykle se tato čísla nazývají frekvenční přihrádky. takže výstupní hodnota může být kdekoli v rámci specifikovaných přihrádek.
Rychlost:
pro Arduino nano to vyžaduje:
16 bodů: 4 ms32 bodů: 10 ms 64 bodů: 26 ms 128 bodů: 53 ms
Krok 6: Závěr
Tento kód FFT lze použít v aplikacích v reálném čase. Dokončení výpočtu trvá přibližně 30 ms. Jeho rozlišení je však omezeno řadou vzorků. Počet ukázek je omezen pamětí Arduino. Použitím Arduino Mega nebo jiného vyššího výkonu lze zlepšit přesnost desky.
pokud máte nějaké dotazy, návrhy nebo opravy, neváhejte je komentovat.
Aktualizace (2/5/21)
Aktualizace: // ----------------------------- Funkce FFT --------------- ------------------------------- // float FFT (int v , int N, float Frequency)
Datový typ N se změnil na Integer (stávající bajt), aby podporoval> 255 velikosti vzorku. Pokud je velikost vzorku <= 128, měl by být použit datový typ byte.
Doporučuje:
Super FAST RC Ground Effect Vehicle (Ekranoplan): 5 kroků (s obrázky)

Super FAST RC Ground Effect Vehicle (Ekranoplan): Víte, jak se letadla během přistání na chvíli vznáší několik stop nad zemí, než jejich kola skutečně narazí na přistávací dráhu? To má cestujícím nejen zajistit hladké přistání, ale je to také přirozený výsledek pozemního efektu, při kterém
Transform-a-Car: Dálkově ovládané na samočinné: 4 kroky

Transform-a-Car: Remote Controlled to Self Controlled: This is a hack on a RC car with a broken remote. Při garážových výprodejích toho najdete spoustu
QuickFFT: Vysokorychlostní FFT pro Arduino: 3 kroky

QuickFFT: Vysokorychlostní FFT pro Arduino: Typické Arduino má omezenou RAM a výpočetní výkon a FFT je výpočetně náročný proces. U mnoha aplikací v reálném čase je jediným požadavkem získat frekvenci s maximální amplitudou nebo požadovanou pro detekci frekvenčních špiček. V jednom z
1024 vzorků FFT spektrálního analyzátoru pomocí kroků Atmega1284: 9

1024 vzorků FFT spektrálního analyzátoru pomocí Atmega1284: Tento relativně snadný návod (s ohledem na složitost tohoto předmětu) vám ukáže, jak lze pomocí desky typu Arduino (1284 Narrow) a sériového plotru vytvořit velmi jednoduchý spektrální analyzátor 1024 vzorků. Jakýkoli druh Arduino Compa
Použijte 1 analogový vstup pro 6 tlačítek pro Arduino: 6 kroků
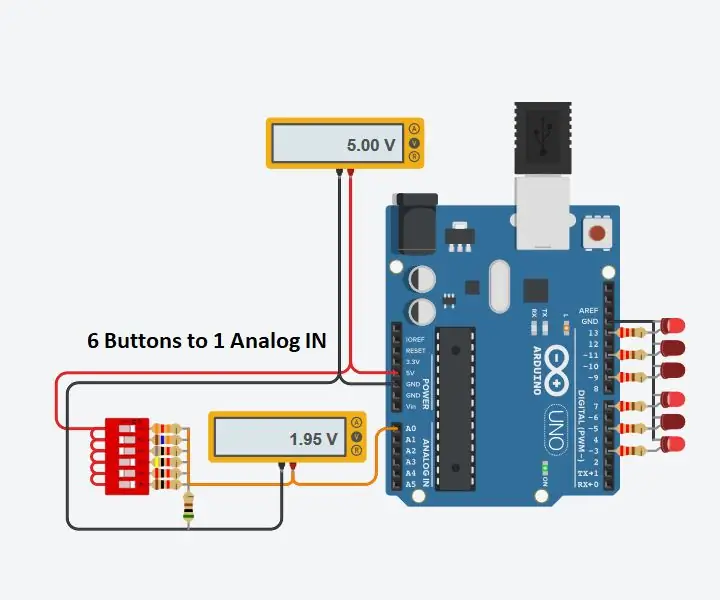
Použijte 1 analogový vstup pro 6 tlačítek pro Arduino: Často jsem přemýšlel, jak bych mohl pro svůj Arduino získat více digitálních vstupů. Nedávno mě napadlo, že bych měl být schopen použít jeden z analogových vstupů pro zavedení více digitálních vstupů. Rychle jsem hledal a zjistil, kde jsou lidé
