Obsah:
- Krok 1:
- Krok 2:
- Krok 3: Fázorový diagram napětí a proudu pro křivky
- Krok 4: Proudové, odporové a napěťové fázové úhly obvodů řady RC
- Krok 5: Impedance a fázový úhel obvodů řady RC
- Krok 6: Variace impedance s frekvencí
- Krok 7: Variace impedance a fázového úhlu s frekvencí
- Krok 8: Ukázka toho, jak se Z a XC mění s frekvencí
- Autor John Day day@howwhatproduce.com.
- Public 2024-01-30 08:19.
- Naposledy změněno 2025-01-23 14:38.

RC obvody
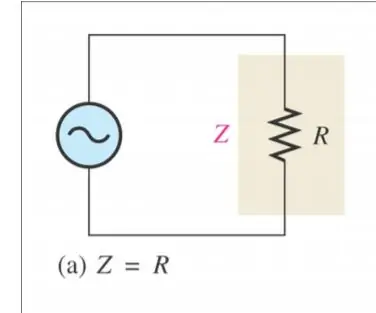
Impedance: je to, co zdroj „vidí“jako úplný odpor vůči proudu
Způsob výpočtu impedance se liší od jednoho obvodu
Krok 1:

Když je obvod čistě kapacitní (obsahuje pouze kondenzátor), fázový úhel mezi aplikovaným napětím a celkovým proudem je 90 ° (proudové vývody)
Krok 2:

Pokud je v obvodu kombinace odporu a kapacity, fázový úhel mezi odporem (R) a kapacitní reaktancí (XC) je 90 ° a fázový úhel pro celkovou impedanci (Z) je někde mezi 0 ° a 90 °
Pokud je v obvodu kombinace odporu i kapacity, fázový úhel mezi celkovým proudem (IT) a napětím kondenzátoru (VC) je 90 ° a fázový úhel mezi aplikovaným napětím (VS) a celkovým proudem (IT) je někde mezi 0 ° a 90 °, v závislosti na relativních hodnotách odporu a kapacity
Krok 3: Fázorový diagram napětí a proudu pro křivky

Krok 4: Proudové, odporové a napěťové fázové úhly obvodů řady RC

Krok 5: Impedance a fázový úhel obvodů řady RC

- V sériovém RC obvodu je celková impedance fázorovým součtem R a Xc
- Impedanční velikost: Z = √ R^2 + Xc^2 (vektorový součet)
- Fázový úhel: θ = tan-1 (X C/R)
Proč používáme vektorový součet ne algebraický součet?
Odpověď: Protože odpor nezpomaluje napětí, ale kondenzátor to dělá.
Takže Z = R+Xc je špatně.
Aplikace Ohmova zákona na RC obvod celé řady zahrnuje použití veličin Z, Vs a Itot jako:
Itot = Vs/Z Z = Vs/Itot Vs = Itot * Z
Nezapomeňte také:
Xc = 1/2πFC
Krok 6: Variace impedance s frekvencí

Krok 7: Variace impedance a fázového úhlu s frekvencí

Krok 8: Ukázka toho, jak se Z a XC mění s frekvencí

R zůstává konstantní
Doporučuje:
VYROBTE SVÉ OKRUHOVÉ OBVODY ARKÁDOVÁ VENTILÁTORKA ŘEKNĚTE IU: 5 kroků

UDĚLÁVEJTE SVÉ OKRUHOVÉ OBVODY ARKÁDOVÝ SADU ŘEKNOUT I <3 U: Nyní můžete nastavit arkádovou sadu snap obvodů tak, že pomocí tohoto pokynu MILUJU U! Také se přihlašuji do této soutěže v srdci! Doufám, že vyhraju
Vytvořte prkénko pro elektronické obvody - Papercliptronics: 18 kroků (s obrázky)

Vytvořte prkénko pro elektronické obvody-Papercliptronics: Jedná se o SILNÉ a PERMANENTNÍ elektronické obvody. Aktuální aktualizace najdete na adrese papercliptronics.weebly.com Užijte si náš podrobný návod na vytváření domácích elektronických obvodů
Prototypovací sada pro obvody z E-textilu: 5 kroků
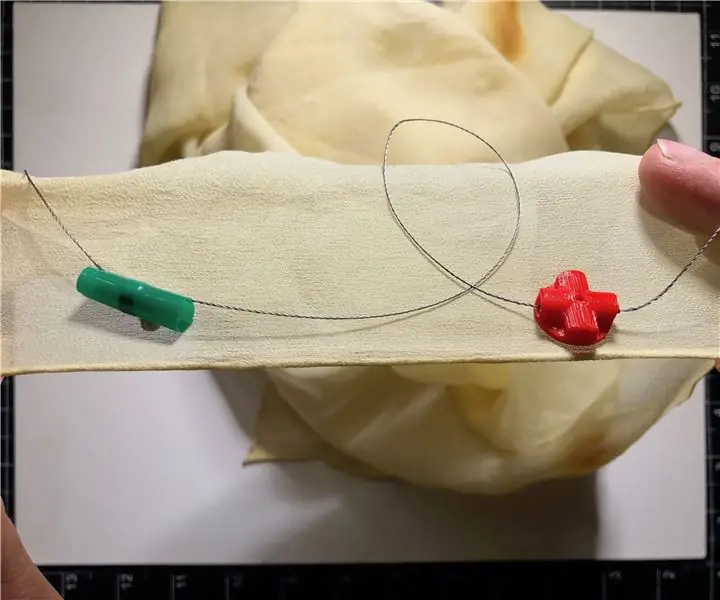
Prototypovací sada pro obvody z e-textilu: Tento návod vás naučí, jak vytvořit jednoduchou soupravu pro prototypování obvodů z e-textilu. Tato sada se skládá z vodičů a spojovacích bodů, které jsou opakovaně použitelné, ale robustní. Cílem tohoto projektu je poskytnout výrobcům e-textilu systém, který
Pasivní dolní propust pro zvukové obvody (RC filtr volného tvaru): 6 kroků

Pasivní nízkoprůchodový filtr pro zvukové obvody (RC filtr Free-Form): Jedna věc, která mi vždy dělala problémy při výrobě elektronických nástrojů na míru, je trvalé rušení mých zvukových signálů. Zkoušel jsem stínění a různé triky pro zapojení signálů, ale nejjednodušší řešení post-build se zdá být
Přizpůsobte integrované obvody SMD Breadboard!: 10 kroků (s obrázky)

Přizpůsobte integrované obvody SMD Breadboard!: Mnohokrát se stává, že náš oblíbený integrovaný obvod je k dispozici pouze v balíčku SMD a neexistuje způsob, jak jej vyzkoušet na prkénku. V tomto krátkém návodu bych vám ukázal způsob, jakým jsem si vyrobil tento malý adaptér pro SMD IC tak, aby mohl
